多目标跟踪中的数据关联代码实践(上)

---

前言

接下来我们将对多目标跟踪任务中的数据关联算法进行研究，我将结合一些文献和自己的理解，利用一些工具对相关数据关联算法进行实验，包括基于IOU的贪婪匹配、基于匈牙利和KM算法线性偶图匹配、基于图论的离线数据关联(主要介绍最小代价流)以及最新的一些基于深度学习的端到端数据关联网络。代码我都会随博客一起发到github。

1 背景简介

之前我们也说到，目前主流的MOT框架是DBT框架，这种框架的特点就是离不开数据关联算法，不论是对不同帧之间跟踪轨迹的关联还是跟踪轨迹和观测量的关联， 有数据关联才能更好的保证目标ID的连续性。数据关联算法以偶图匹配类为主，尤其是在离线跟踪中存在有大量基于图论的算法，比如：最小代价流、最大流、最小割、超图等等。而近两年也出现了一批端到端的数据关联算法，对于这一点呢，有几个很大的问题，一个是数据关联是一个n:m的问题，而网络对于输出的尺寸一般要求是固定的，如果构建关联矩阵是一个问题。另外，数据关联从理论上来讲是一个不可导的过程，其包含有一些排序的过程，如何处理这一点也很重要。

2 基于IOU的贪婪匹配

2.1 IOU Tracker & V-IOU Tracker

不得不说IOU Tracker和他的改进版V-IOU Tracker算是多目标跟踪算法中的一股清流，方法特别简单粗暴，对于检测质量很好的场景效果比较好。首先我们交代一下IOU的度量方式：

$$ IOU\left( {a,b} \right) = \frac{{Area\left( a \right) \cap Area\left( b \right)}}{{Area\left( a \right) \cup Area\left( b \right)}} $$
IOU Tracker的跟踪方式没有跟踪，只有数据关联，关联指标就是IOU，关联算法就是一种基于IOU的贪婪匹配算法：

这里我们留到下一节将，我会利用不同的贪婪方式进行IOU匹配。那么V-IOU的改进就是，由于IOU Tracker仅仅是对观测量进行了关联，当目标丢失或者检测不到的时候，便无法重建轨迹，因此V-IOU加入了KCF单目标跟踪器来弥补这一漏洞，也很粗暴。。

2.2 IOU Matching

基于贪婪算法的数据关联的核心思想就是，不考虑整体最优，只考虑个体最优。这里我设计了两种贪婪方式，第一种Local IOU Matching,即依次为每条跟踪轨迹分配观测量，只要IOU满足条件即可，流程如下：

IOU Tracker就是采用的这种局部贪心方式，这种贪心策略的特点是每次为当前跟踪轨迹选择与之IOU最大的观测量。那么我们再提出一种全局的贪婪策略，即每次选择所有关联信息中IOU最大的匹配对，流程如下：

这两种贪婪方式的代码如下：

def GreedyAssignment(cost, threshold = None, method = 'global'):
    """Using iou matching to make linear assignment

    Parameters
    ----------
    cost : ndarray
        A NxM matrix for costs between each track_ids with dection_ids
    threshold: float
        if cost > threshold, then will not be considered
    method: str
        eg: global, local

    Returns
    -------
    row_idx: List of matched tracks (<=N,)
        assigned tracklets' id
    col_idx: List of matched dets (<=M,)
        assigned dets' id
    unmatched_rows: List of unmatched tracks
        unassigned tracklets' id
    unmatched_cols: List of unmatched dets
        unassigned dets' id
    """
    cost_c = np.atleast_2d(cost)
    sz = cost_c.shape

    if threshold is None:
        threshold = 1.0

    row_idx = []
    col_idx = []
    if method == 'global':
        vector_in = list(range(sz[0]))
        vector_out = list(range(sz[1]))
        while min(len(vector_in), len(vector_out)) > 0:
            v = cost_c[np.ix_(vector_in, vector_out)]
            min_cost = np.min(v)

            if min_cost <= threshold:
                place = np.where(v == min_cost)
                row_idx.append(vector_in[place[0][0]])
                col_idx.append(vector_out[place[1][0]])
                del vector_in[place[0][0]]
                del vector_out[place[1][0]]
            else:
                break
    else:
        vector_in = []
        vector_out = list(range(sz[1]))
        index = 0
        while min(sz[0] - len(vector_in), len(vector_out)) > 0:
            if index >= sz[0]:
                break
            place = np.argmin(cost_c[np.ix_([index], vector_out)])

            if cost_c[index, vector_out[place]] <= threshold:
                row_idx.append(index)
                col_idx.append(vector_out[place])
                del vector_out[place]
            else:
                vector_in.append(index)
            index += 1
        vector_in += list(range(index, sz[0]))

    return np.array(row_idx), np.array(col_idx), np.array(vector_in), np.array(vector_out)

下面我们先看看两种方式的跟踪效果：

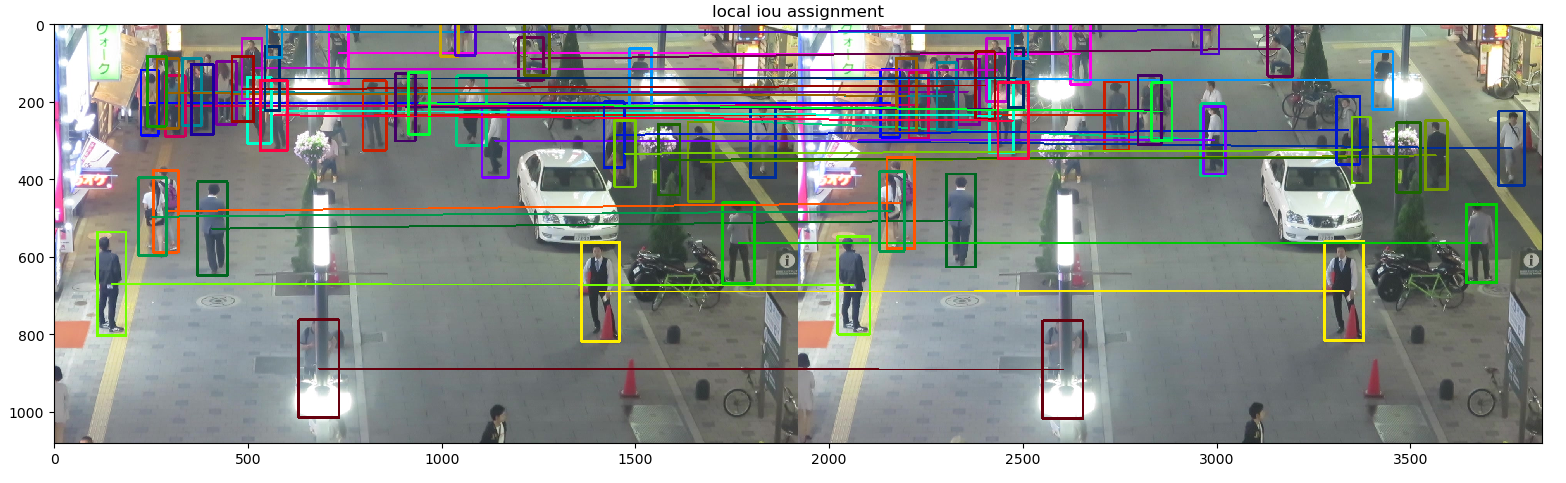
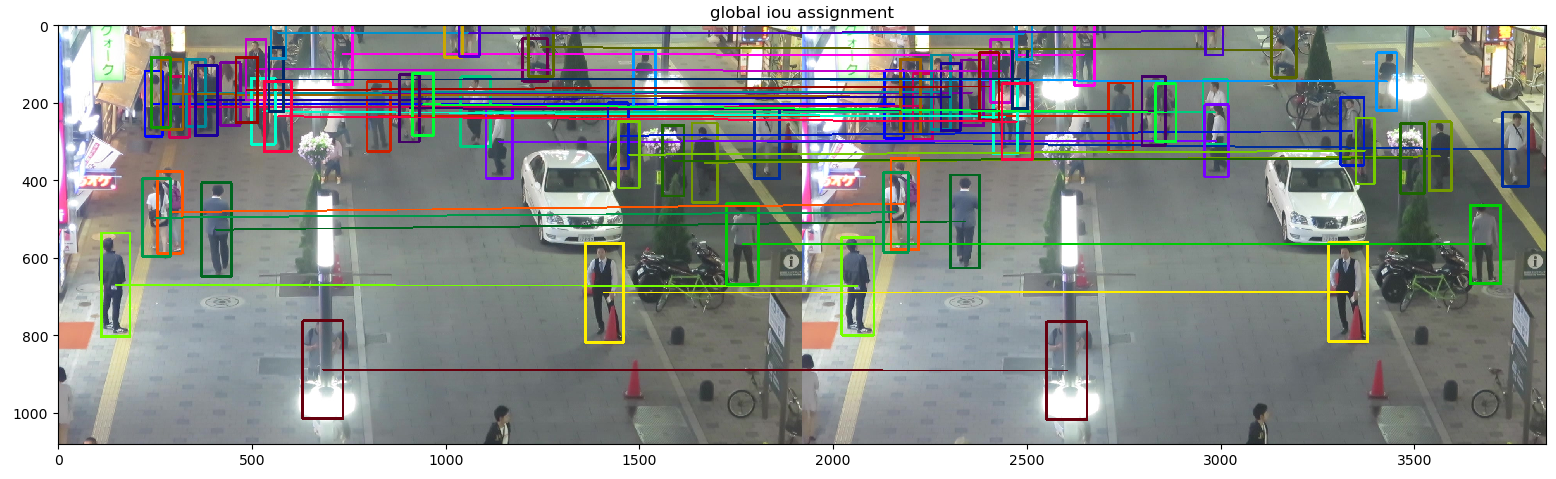
可以看到跟踪效果并不是很差，那么我们观察二者定量的结果则为：

Local: MOTA=0.77, IDF1=0.83

Global: MOTA=0.79, IDF1=0.88

相比之下全局的贪心策略比局部的要好

3 线性分配

3.1 匈牙利算法和KM算法简介

线性分配问题也叫指派问题，通常的线性分配任务是给定N个workers和N个tasks，结合相应的N×N的代价矩阵，就能得到匹配组合。其模型如下：

$$ \begin{array}{l} min = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{C_{ij}}{x_{ij}}} } \\ s.t.\left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{x_{ij}}} = 1\\ \sum\limits_{j = 1}^N {{x_{ij}}} = 1\\ {x_{ij}} = 0\;or\;1 \end{array} \right. \end{array} $$
上述模型有个问题，即要求workers和tasks的数量对等，然而在MOT问题中待匹配的跟踪轨迹和检测数量大概率不相同，而且我们经常还会设定阈值来限制匹配。

匈牙利算法是专门用来求解指派问题的算法，并且通常用于求解二分图最大匹配的。也就是说我们需要先利用规则判断边是否连接，然后匹配，因此不会出现非边节点存在匹配，只有可能出现剩余未匹配：

$$ \begin{array}{l} max = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{L_{ij}}{x_{ij}}} } \\ s.t.\left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{x_{ij}}} \le 1\\ \sum\limits_{j = 1}^M {{x_{ij}}} \le 1\\ {x_{ij}} = 0\;or\;1 \end{array} \right. \end{array} $$
匈牙利算法的问题在于一旦确定边之后就没有相对优劣了，所以我们这里介绍带权二分图匹配KM，顾名思义，就是求最小代价，只不过是不对等匹配：

$$ \begin{array}{l} min = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{C_{ij}}{x_{ij}}} } \\ s.t.\left\{ \begin{array}{l} \sum\limits_{i = 1}^N {{x_{ij}}} {\rm{ = }}1\\ \sum\limits_{j = 1}^M {{x_{ij}}} \le 1\\ {x_{ij}} = 0\;or\;1 \end{array} \right. \end{array} $$
这里我们可以看到有一个维度的和要求是1，原因就是必须要保证有一个维度满分配，不然就会直接不建立连接了。

3.2 实验对比

这里我们借用scipy工具箱实现：

inf_cost = 1e+5

def LinearAssignment(cost, threshold = None, method = 'KM'):
    """Using Hungarian or KM algorithm to make linear assignment

    Parameters
    ----------
    cost : ndarray
        A NxM matrix for costs between each track_ids with dection_ids
    threshold: float
        if cost > threshold, then will not be considered
    method : str
        'KM': weighted assignment
        'Hungarian': 01 assignment

    Returns
    -------
    row_idx: List of matched tracks (<=N,)
        assigned tracklets' id
    col_idx: List of matched dets (<=M,)
        assigned dets' id
    unmatched_rows: List of unmatched tracks
        unassigned tracklets' id
    unmatched_cols: List of unmatched dets
        unassigned dets' id
    min_cost: float
        cost of assignments
    """
    cost_c = deepcopy(np.atleast_2d(cost))
    sz = cost_c.shape

    if threshold is not None:
        cost_c = np.where(cost_c > threshold, inf_cost, cost_c)

    if method == 'Hungarian':
        t = threshold if threshold is not None else inf_cost
        cost_c = np.where(cost_c < t, 0, cost_c)

    # linear assignment
    row_ind, col_ind = linear_sum_assignment(cost_c)
    if threshold is not None:
        t = inf_cost - 1 if threshold == inf_cost else threshold
        mask = cost_c[row_ind, col_ind] <= t
        row_idx = row_ind[mask]
        col_idx = col_ind[mask]
    else:
        row_idx, col_idx = row_ind, col_ind

    unmatched_rows = np.array(list(set(range(sz[0])) - set(row_idx)))
    unmatched_cols = np.array(list(set(range(sz[1])) - set(col_idx)))

    min_cost = cost[row_idx, col_idx].sum()

    return row_idx, col_idx, np.sort(unmatched_rows), np.sort(unmatched_cols), min_cost

同样地，为了更好地对比，我们以IOU为代价指标，分别以匈牙利算法和KM算法为数据关联算法进行实验，有意思的是对于MOT-04-SDP视频而言，二者并没有太大区别，整体效果跟Global IOU Assignment一致。

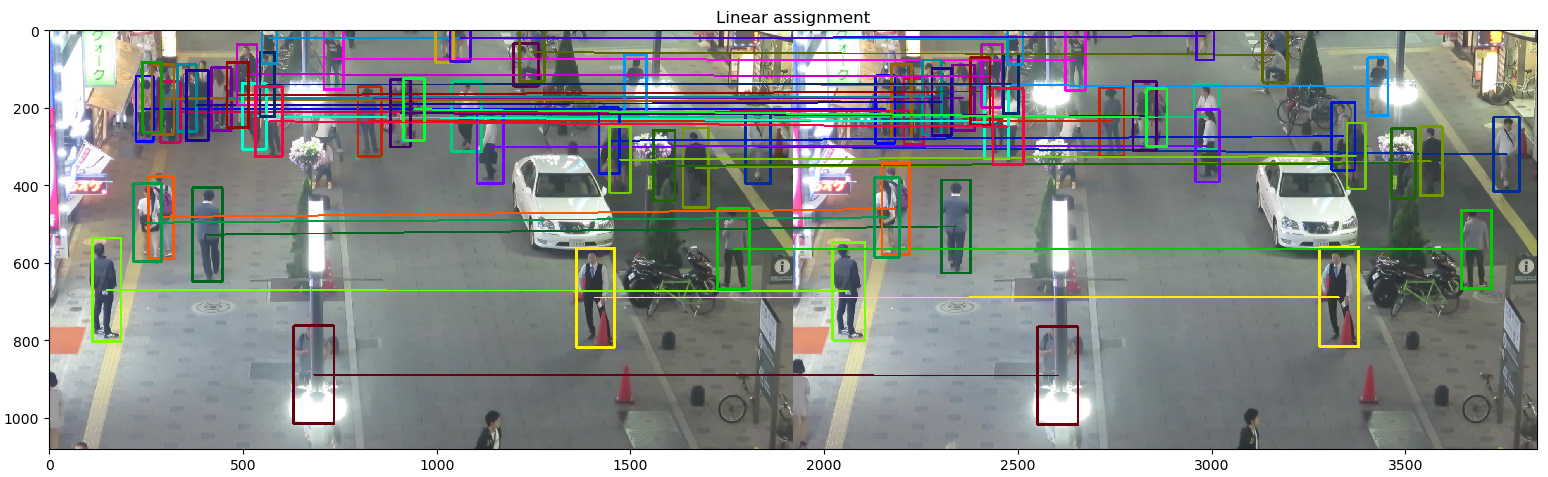
以上代码我都放到了github。