前言
接下来我们将对多目标跟踪任务中的数据关联算法进行研究,我将结合一些文献和自己的理解,利用一些工具对相关数据关联算法进行实验,包括基于IOU的贪婪匹配、基于匈牙利和KM算法线性偶图匹配、基于图论的离线数据关联(主要介绍最小代价流)以及最新的一些基于深度学习的端到端数据关联网络。代码我都会随博客一起发到github。
4 最小代价流
4.1 算法形式
在了解最小代价流之前,我们需要先铺垫一下几个常见图模型,以帮助我们理解,比如最短路、最大流、最小费用最大流,最小割(闭嘴,我暂时没看懂)。下图是一个很常见的图网络:
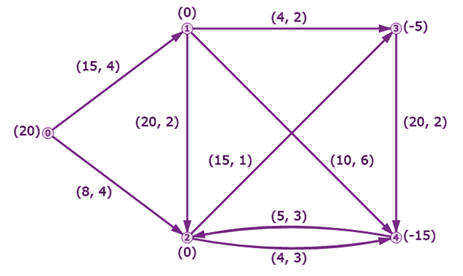
我们可以看到,图上有很多节点和边,这两个元素是组成图模型的核心。其次,每条边上都会有对应的数值,比如最短路问题中的相邻两节点的距离,最大流中的边容量,最小费用最大流问题中的边容量和费用。那么我们来看看几个问题的具体定义:
- 最短路问题
最短路问题一般特指单源单汇最短路问题,即给定起点和终点,从各种路径中选择最短的路径。
$$ \begin{array}{l} min = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{W_{ij}}{x_{ij}}} } \\ s.t.\left\{ \begin{array}{l} \sum\limits_{j = 1}^N {{x_{ij}} - \sum\limits_{k = 1}^N {{x_{ki}}} } {\rm{ = }}\left\{ \begin{array}{l} 1,i = 1\\ - 1,i = N\\ 0,i \ne 1,N \end{array} \right.\\ {x_{ij}} = 0\;or\;1 \end{array} \right. \end{array} $$
上面公式中如果结合图模型来思考会简单很多,即中间节点无论会不会通过,其流入边和流出边一定有且只有0或1个,不可能经过这个点而不经过与之相邻的边。不过对于起点和终点则允许有一条流出边或一条流入边。
- 最大流问题
最大流问题就是选择从起点到终点的最大流量分配,与最短路的最大区别在于最短路问题中每个节点只能选择一条流出边和一条流入边,而最大流问题则只要满足边容量限制,则可任意选择流入流出边数量。
$$ \begin{array}{l} max = v\left( f \right) = \sum\limits_j {{f_{sj}}} - \sum\limits_i {{f_{is}}} \\ s.t.\left\{ \begin{array}{l} \sum\limits_j {{f_{ij}}} = \sum\limits_k {{f_{ki}}} \\ \sum\limits_j {{f_{sj}}} = \sum\limits_k {{f_{kt}}} = v\left( f \right)\\ 0 \le {f_{ij}} \le {w_{ij}} \end{array} \right. \end{array} $$
上面公式的意思是,即中间节点无论会不会通过,其流入边流量之和=流出边流量之和,从起点流出的总流量=流入终点的总流量,每条边的流量有上限。
- 最小费用流问题
最小费用流的约束条件和最大流的一样,只不过为了更好描述目标函数我改写成了类似于最短路问题的形式。其目标是选择费用最短的流,当然,它跟最大流问题不同,这里需要设置起始点的流出流量,而且,如果在最大流限制下求解最小费用流,那么就是最小费用最大流问题了。
$$ \begin{array}{l} min = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{C_{ij}}{x_{ij}}} } \\ s.t.\left\{ \begin{array}{l} \sum\limits_{j = 1}^N {{x_{ij}} - \sum\limits_{k = 1}^N {{x_{ki}}} } {\rm{ = }}\left\{ \begin{array}{l} 负数,i = 1\\ 正数,i = N\\ 0,i \ne 1,N \end{array} \right.\\ 0 \le {x_{ij}} \le {w_{ij}} \end{array} \right. \end{array} $$
联系到多目标跟踪任务,其数据关联任务从短期来看就是一个二分图匹配问题,从长期来看就是一个图网络模型。
(1)如果我们要用最短路模型来描述数据关联问题,其节点就是跟踪对象id,边代表跟踪轨迹和检测之间的代价。那单源单汇最短路模型就远远不足以描述,因为跟踪轨迹和检测数量是大于1的,所以从形式上来讲是多源多汇最短路,但是最短路没有限制中间节点的可重复性,所以这个问题应该用路由问题中的K –最短不相交路线(K shortest disjoint paths)来描述;
(2)如果我们要用最大流模型来描述该问题,那么不同于最短路,边容量代表跟踪轨迹和检测之间的连接可能性,所以只可能是0和1。最终要求的就是最大流量,由于边容量的限制,所以不可能重复,也就是最多可能轨迹。而且这么看来,匈牙利算法很像是最大流模型的特例;
(3)如果我们要用最小费用流模型来描述该问题,那么就跟第一部分中的最短路问题一样了,只不过多源多汇问题变成了给定初始流量的情形,距离变成了费用。最大的区别在于需要合理设定初始流量(代表了最终有多少条轨迹),还要设定边容量,不然容易所有流都流向同一条边;
(4)结合(2)(3)来看,最大流模型只需要设定跟踪轨迹和检测的连接可能性,但是缺乏了相对性。而最小费用流则只需要设定代价值,但是需要设定初始流量。这里的初始流量代表了轨迹数量,所以先用最大流模型求出最大流,即可作为初始的轨迹数量,然后再求最小费用流即可,也就是最小费用最大流。不过两个任务都有着相同的任务,那就是寻找目标轨迹,所以这样来说时间效率会较低。一般来说我们会直接使用最大流模型/最小割模型,或者直接使用最小费用流+搜索算法。
总的来说,最大流模型的优点是参数量少,但是确定跟匈牙利算法一样,我们无法对于0.9和0.5相似度的边进行相对选择,因为都是1。最小费用流模型的优点是保留了相似度,但是初始流量这一超参数不好设定。K-最短不相交路模型跟最小费用流一样,都需要设定轨迹数量。所以我们会选择用搜索算法使用最小费用流,通过搜索阈值使用最大流模型.
4.2基于最大化后验概率模型的网络流建图
对于最小费用流而言,最难的地方在于设定初始流量和边容量,使得跟踪轨迹不交叉,而且跟踪轨迹尽可能多而合理。最重要的是,我们不知道在网络模型中哪个节点是轨迹的起点或者终点,这些都需要我们去建模。再加上我们的目标是使得代价最小,极可能最终出现每条轨迹只有一个节点的情形。
下面我们要设定几个代价值,由于每个点都有属于轨迹起点和终点的可能性,所以网络会非常大,为了更好地借鉴已有的最小费用流模型,我们可以转化为单一起点和终点的网络图:
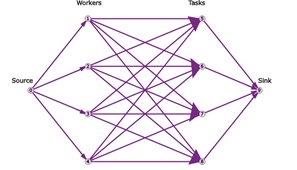
我们可以看到,简单的最小代价流结构存在几个问题:
一开始我们就要选定哪些节点有可能成为起点,哪些节点有可能成为终点,这无疑增加了参数量;
类似于最大流模型,我们通过设定边容量为1可以保证每条边最多被选择一次。但是,我们无法确保最多只有一个节点可以连接到目标节点,这就不能保证跟踪轨迹的不重叠。
针对以上问题,我们可以引入过渡节点的概念,同时也就引入了过渡边,每个节点连接一条过渡边,这样通过设定过渡边容量,可以限制每个节点的流出流量,相应地就可以限制最多只有一个节点可以连接到目标节点。而且,我们让每个节点都连接起点,每个节点的过渡节点连接终点,这样就保证上面两个问题都解决了。具体网络结构如下:
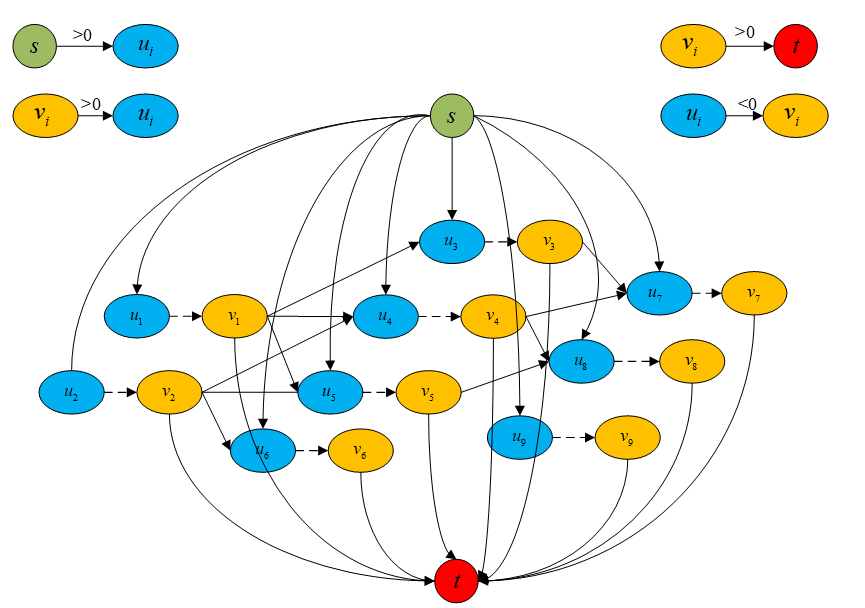
我们可以看到每个节点u都连接了起点,每个节点v都连接了终点,每个节点u都连接了过渡节点v。正如我们之前说的,每条边容量都是1,可以有效防止轨迹重叠。另外我在图中注明了每条边费用的取值范围,我们定义每条包含起点和终点的边的费用都是比较大的正数,节点与过渡节点的边的费用是负数,这样可以避免过早的终止轨迹,过渡节点与节点之间的边的费用就是跟踪轨迹和检测的代价值,取正数,不然每条轨迹都会在最后一帧终止。所以这里的参数有:初始流量的大小(轨迹数量)、节点属于轨迹起点/终点的概率、节点到过渡节点的补偿(选择这个节点的补偿)、过渡节点到节点的概率(匹配代价)。
下面我们联系多目标跟踪模型的形式来为这些参数赋予特殊的含义,首先给出后验概率形式,T表示已有轨迹,Z表示观测值:
$$ \begin{array}{l} {T^ * } = \mathop {argmax}\limits_T P\left( {\left. T \right|Z} \right)\\ \;\;\;\; = \mathop {argmax}\limits_T \frac{{P\left( {\left. Z \right|T} \right)P\left( T \right)}}{{P\left( Z \right)}}\\ \;\;\;\; = \mathop {argmax}\limits_T \frac{{\prod\limits_i {P\left( {\left. {{z_i}} \right|T} \right)P\left( T \right)} }}{{P\left( Z \right)}} \end{array} $$
如果我们不考虑目标之间的联系,即假设目标相互独立,将联系归于代价值之中。那么上式就可以转化为:
$$ {T^ * } = \mathop {argmax}\limits_T \frac{{\prod\limits_i {P\left( {\left. {{z_i}} \right|T} \right)P\left( T \right)} }}{{\prod\limits_i {P\left( {{z_i}} \right)} }} = \mathop {argmax}\limits_T \prod\limits_i {\frac{{P\left( {\left. {{z_i}} \right|T} \right)P\left( T \right)}}{{P\left( {{z_i}} \right)}}} $$
这里我们就需要了解三个概率:
$$ \left\{ \begin{array}{l} P\left( {{z_i}} \right) = {\theta _i}\\ P\left( {\left. {{z_i}} \right|T} \right) = P\left( {\left. {{z_i}} \right|\left\{ {{x_{{k_0}}},{x_{{k_1}}},...,{x_{{k_{{l_k}}}}}} \right\}} \right)\\ P\left( {{T_k}} \right) = P\left( {\left\{ {{x_{{k_0}}},{x_{{k_1}}},...,{x_{{k_{{l_k}}}}}} \right\}} \right)\\ \;\;\;\;\;\;\;\;\;\; = {P_s}\left( {{x_{{k_0}}}} \right)P\left( {\left. {{x_{{k_1}}}} \right|{x_{{k_0}}}} \right)P\left( {\left. {{x_{{k_2}}}} \right|\left\{ {{x_{{k_0}}},{x_{{k_1}}}} \right\}} \right)...P\left( {\left. {{x_{{k_{{l_k}}}}}} \right|\left\{ {{x_{{k_0}}},{x_{{k_1}}},...,{x_{{k_{{l_{k - 1}}}}}}} \right\}} \right) \end{array} \right. $$
另外,我们还需要补充节点的概念来完善数据关联模型,因为上面的几个概念中我们还没有加入轨迹的终点的概率,所以明确一下联合概率数据关联模型:
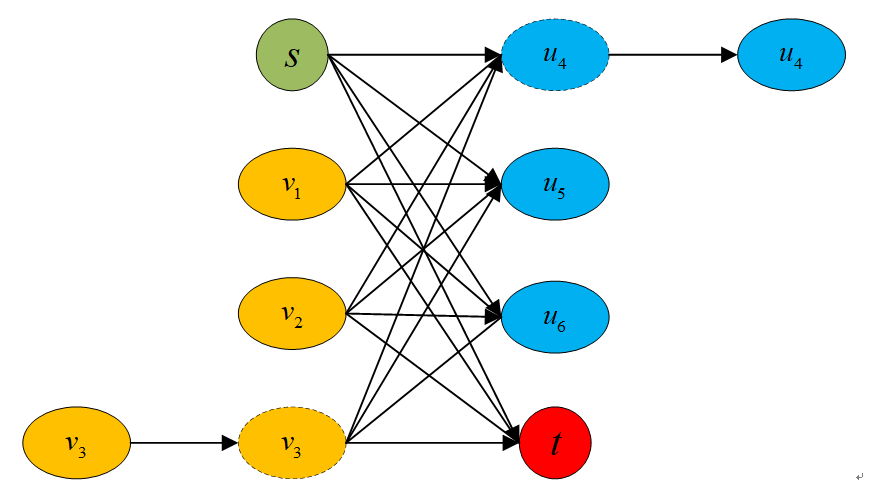
上图中虚线部分代表非当前时刻的节点,这样我们就将虚警和杂波利用起点和终点消除了,由于我们可以跨帧连接,所以虚拟目标就可以近似忽略。
接下来我们开始分析概率模型,我们可以利用对数似然概率来描述:
$$ \begin{array}{l} {T^ * } = \mathop {argmax}\limits_T \prod\limits_i {\frac{{P\left( {\left. {{z_i}} \right|T} \right)P\left( T \right)}}{{P\left( {{z_i}} \right)}}} \\ \;\;\;\; = \mathop {argmin - ln}\limits_T \prod\limits_i {\frac{{P\left( {\left. {{z_i}} \right|T} \right)P\left( T \right)}}{{P\left( {{z_i}} \right)}}} \\ \;\;\;\; = \mathop {argmin}\limits_T \sum\limits_i {\left( { - ln\left[ {P\left( {\left. {{z_i}} \right|T} \right)} \right] - ln\left[ {P\left( T \right)} \right] + ln\left[ {P\left( {{z_i}} \right)} \right]} \right)} \end{array} $$
其中$P\left( {\left. {{z_i}} \right|T} \right)$ 就是当前跟踪轨迹和检测之间的相似度,$P\left( T \right)$就是当前跟踪轨迹存在的概率,$P\left( \right)$表示该观测存在的概率,因为观测有可能是杂波或者虚警,我们可以用于过渡边的代价描述。最后就只剩下${P_s}\left( {{x_{{k_0}}}} \right)$和$P\left( {\left. t \right|T} \right)$两个概率值,这个我们可以当做是一个参数进行试验。就这样,我们最小代价流模型中的每个节点和每条边都赋予了有意义的概念。
4.3 在线和离线跟踪分析
这里我们所说的在线和离线模型的意思是一帧一帧使用min cost flow或者多帧一起优化。对于在线的优化,我们就不需要考虑有多个节点连接同一个节点的特殊情况了,也就是说我们可以直接忽略过渡边,这样就跟KM算法一模一样了,所以我们可以认为匈牙利算法是最大流模型的特殊情况,KM算法是最小费用流的特殊情况。
接下来我们分别对在线和离线的最小代价流模型进行对比实验,其中在线最小代价流模型我们还是采用Kalman+马氏距离的方式构建代价矩阵。而离线的方式下我们则直接使用IOU和HSV直方图作为构建代价矩阵的指标。而对于观测量的概率,即决定过渡边权的指标,我们采用检测的置信度(ln(a*confidence+b))作为指标,而对于起点和终点的判定,我们将其作为超参数,连同代价阈值和特征衰减变量作为超参数。
其中特征衰减变量是对轨迹短暂消失的惩罚:
$$ similarity = similarity \times miss\_rat{e^{time\_gap - 1}} $$
另外,无论是在线跟踪还是离线跟踪,MinCostFlow这个任务本身都需要设定初始流量,也就是跟踪轨迹数量,这个值我们都知道是最少是1,最多是总id数。那么我们就需要用搜索算法来解决,为了保证求解效率,我们简单假设这个问题是一维凸优化问题,采用二分搜索或者斐波那契搜索来进行。
其中二分搜索很简单,对于斐波那契搜索,我们知道斐波那契数列{0,1,1,2,3…},即f(n)=f(n-1)+f(n-2)。对于这个通项公式,我们可以看到对于长度为f(n)的搜索空间,可以将其分为f(n-1)和f(n-2)两个部分,这样就实现了搜索空间的缩减。下面给出具体的算法:

可以看到我上面用了哈希表来存储搜索过程中的结果,避免重复运算,保证O(1)的查询效率。另外,对于求解结果,一般返回的是匹配点对,我们如何将其变成轨迹呢?这就是一个经典的“朋友圈”问题,可以采用并查集来求解,只需要O(n)的时间复杂度和O(n)的空间复杂度。不过我们这个问题简单一点,不存在一个点对应多个点的情况,所以可以简单利用数组或哈希表建立多叉树求解。
4.4 代码实验
为了方便,我们直接用IOU和HSV颜色直方图作为特征进行试验。由于代码太长,我这里这放一部分,其中的Fibonacci搜索过程代码如下:
1 | def fibonacci(self, n): |
跟踪部分代码如下:
1 | def process(self, boxes, scores, image = None, features = None, **kwargs): |
完整版的请前往我的github,下面是我以MOT17-10视频为例跑的结果:

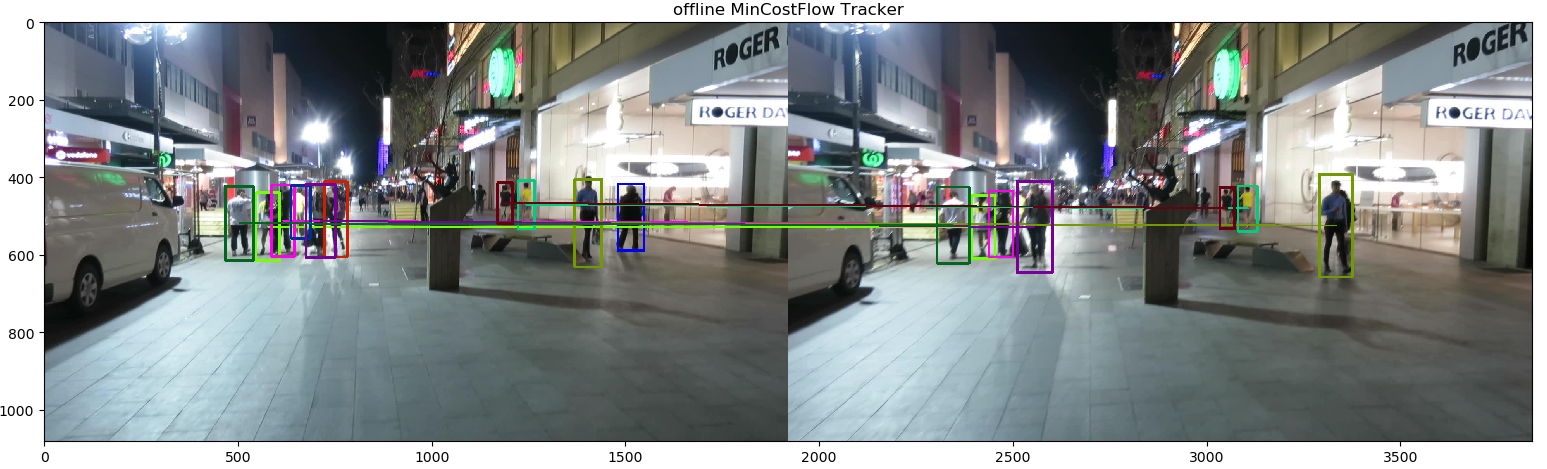
在线MOTA=0.676,离线的MOTA=0.594,离线的特征关联方法很简单,而在线的用的是Kalman+马氏距离。以上都是我自己根据自己理解写的,可能理解有误,也有可能代码实现有问题。
5 基于深度学习的端到端数据关联
近几年由于深度学习框架的兴起,端到端的训练和推理框架展现出一定的数据利用优势,而传统的数据关联算法基本都不满足可导可微的特性,因此出现了很多近似的端到端数据关联框架。这里由于篇幅有限,如果专栏和github反响还可以,后续我会考虑单独开一个基于深度学习的数据关联算法专题,现在我只简要介绍几类出现的框架。
我将近期出现的端到端数据关联框架大致可分为:
- 多特征输入,输出关联矩阵
这类框架只完成了数据关联的任务,即完成对多个目标的匹配,如PAMI2019中的DAN网络结构:
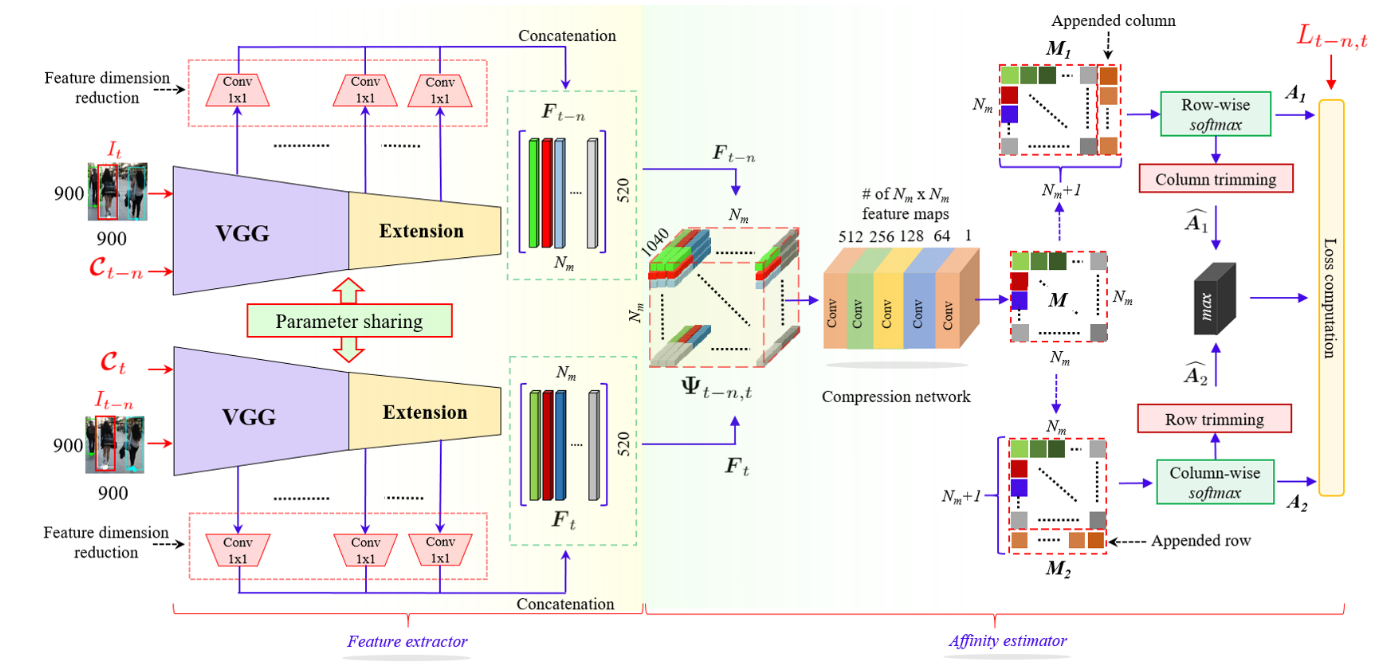
这种框架就是典型的输入历史帧多条跟踪轨迹的特征和当前帧多个特征序列,输出多对多的关联矩阵,这种方式是通过形式的拟合来近似数据关联。又比如ICCV2019的FAMNet:
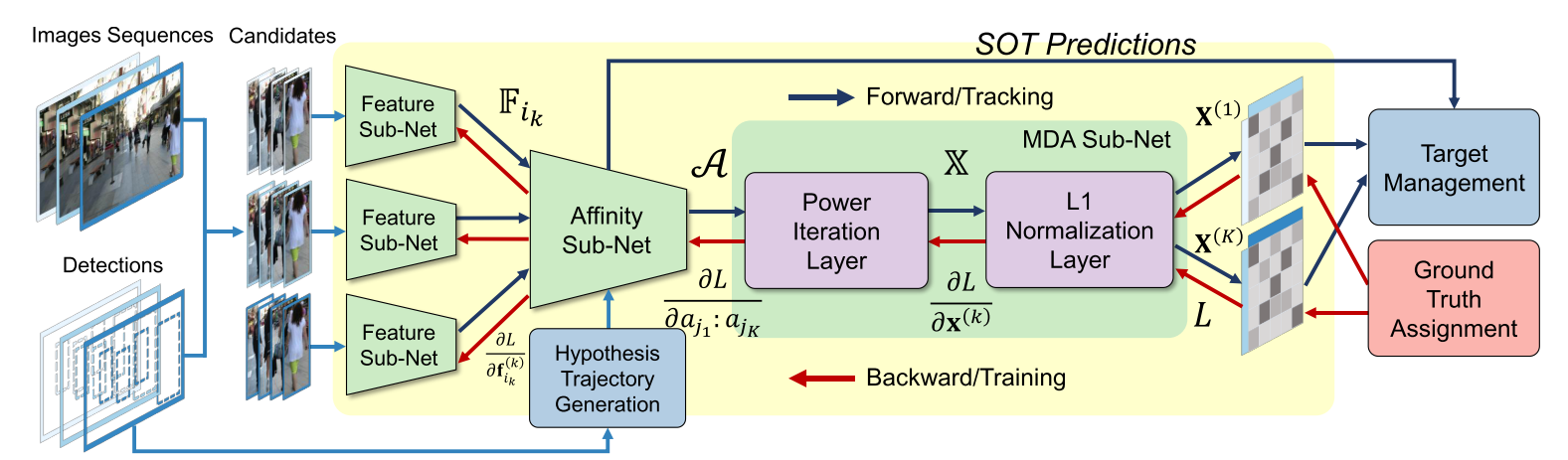
这个框架将SOT和数据关联相集成。综上,这些方法虽然从形式上近似了数据关联算法,但是都要解决两个问题,一个是所有跟踪轨迹和观测的匹配交互,一个是如何过滤虚警和误检。
- 可微数据关联模块
这类框架就是讲传统不可微的数据关联模块改造成可微的模块,比如DeepMOT:

这种方式基于匈牙利算法求解过程中的row-wise和colunm-wise操作,利用Bi-RNN完成全局的关联记忆,最后将关联矩阵通过连续的0~1的数据代替0-1匹配关系,从而实现可微。
- 基于RNN的数据关联预测
这种方式的特点在于,利用过去时间的跟踪记忆,基于不同行人的空间分布进行位置关系预测,比如ICCV2017的AMIR算法:
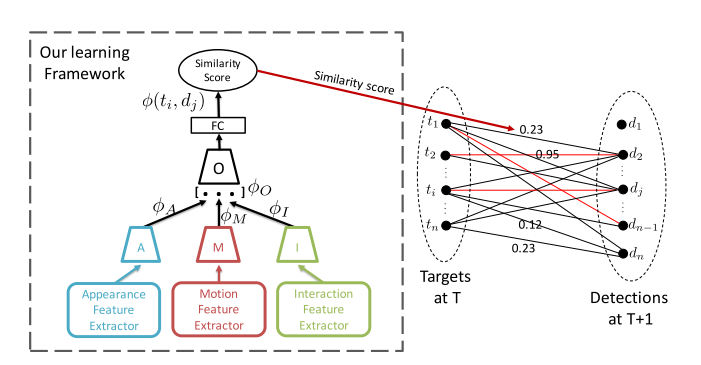
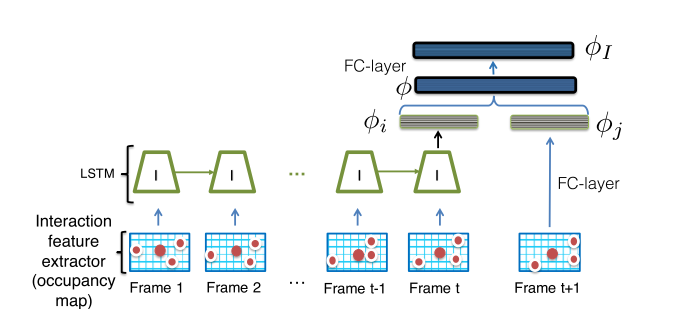
不过这类算法严格来说不能划分为数据关联类算法,这里我提出来肯定是有争议的~
基于图卷积的数据关联
近几年图卷积网络在视觉领域开始热门起来,也有个别团队采用了这种方式,即利用图卷积网络的消息传递机制,模拟离线数据关联的网络图,这种方式的优点在于可以在线学习:
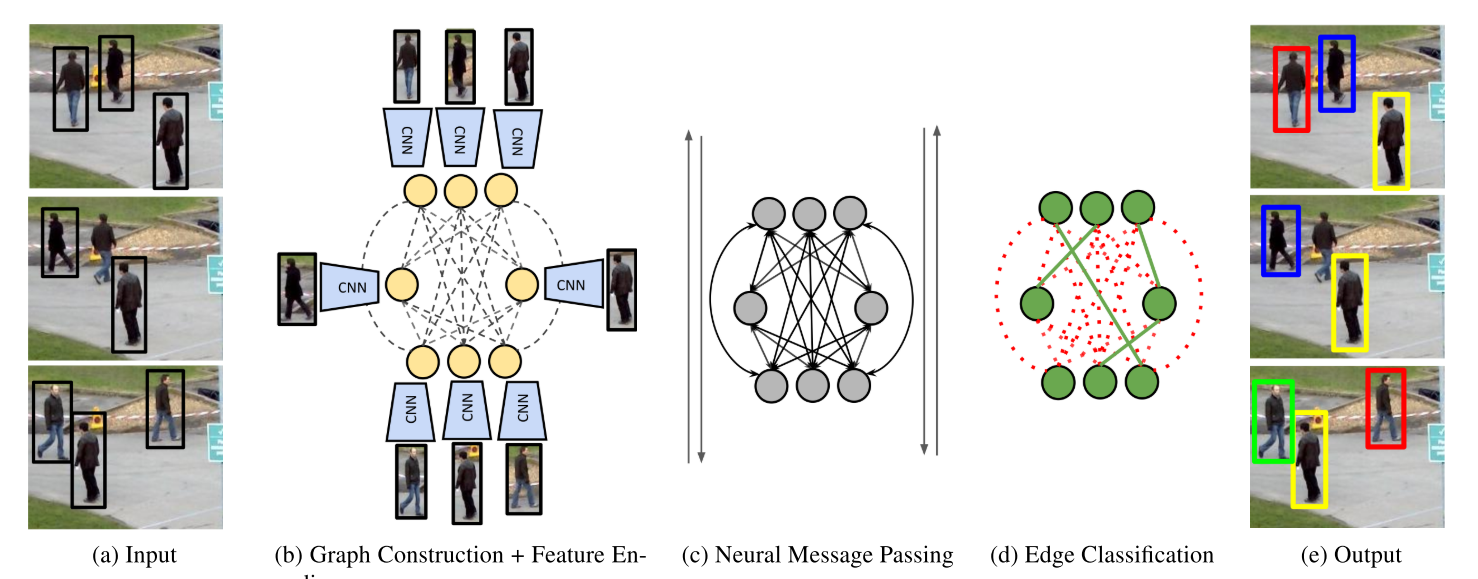
参考资料
[1] SUN S, AKHTAR N, SONG H, et al. Deep affinity network for multiple object tracking[J]. IEEE transactions on pattern analysis and machine intelligence, 2019.
[2] CHU P, LING H. Famnet: Joint learning of feature, affinity and multi-dimensional assignment for online multiple object tracking[C]. in: Proceedings of the IEEE International Conference on Computer Vision. 2019. 6172-6181.
[3] XU Y, BAN Y, ALAMEDA-PINEDA X, et al. DeepMOT: A Differentiable Framework for Training Multiple Object Trackers[J]. arXiv preprint arXiv:1906.06618, 2019.
[4] BRASó G, LEAL-TAIXé L. Learning a Neural Solver for Multiple Object Tracking[J]. arXiv preprint arXiv:1912.07515, 2019.
[5] SADEGHIAN A, ALAHI A, SAVARESE S. Tracking the untrackable: Learning to track multiple cues with long-term dependencies[C]. in: Proceedings of the IEEE International Conference on Computer Vision. 2017. 300-311.

