前言
Kalman滤波器是多目标跟踪任务中一个经典的运动模型,接下来会从理论、发展和代码实践三个方面对其进行展开,本次主要以理论基础为主。 在这篇之前还有一个关于多目标背景任务的介绍,不过被知乎删了,可以去我的博客看
1背景介绍
卡尔曼滤波(Kalman)无论是在单目标还是多目标领域都属于很基础的一种算法,这个是属于自动控制理论中的一种方法,所以对于工科比较容易理解。为了方便理解,我下面对其进行详细的讲解。
首先,卡尔曼滤波器处理的是随机信号,例如,假设我们研究一个房间的温度,依据我们的经验判断,房间温度是恒定的(假设为23℃),但是由于我们的经验不完全可信,所以我们可以引入高斯白噪声来衡量一定的偏差程度(假设上一时刻的偏差是3,但是自己对于预测的不确定度为4,那么此时预测的偏差为5,这里采用的勾股定理)。这时候我们在房间放一个温度计,但是温度计本身也不一定准确,测量值(25℃)与实际值的偏差也视为一种高斯白噪声(假设为4),那么现在同时存在一个根据上一个时刻温度得来的估计量和这个时刻的测量值。
假设这两个值为23℃和25℃,这其实就对应着跟踪问题中的运动估计和实际跟踪结果,此时我们究竟相信谁呢?可利用他们的均方误差来计算:
$$ \begin{array}{l} {H^2} = \frac{{{5^2}}}{{{5^2} + {4^2}}} = 0.78 \Rightarrow T = 23 + 0.78 * \left( {25 - 23} \right) = 24.56\\ Err = \sqrt {\left( {1 - H} \right) * {5^2}} = 2.35 \end{array} $$
由此可将均方误差不断地传递下去,从而估计估算出最优的温度值。
为了方便解释卡尔曼滤波方程,下面以一辆小车的运动为例,假设我们已知上一时刻小车的状态,现在要估计当前时刻的状态:
$$ \begin{array}{l}\left\{ \begin{array}{l}{p_t} = {p_{t - 1}} + {v_{t - 1}} \times \Delta t + \frac{1}{2}{a_t} \times \Delta {t^2}\\{v_t} = {v_{t - 1}} + {a_t} \times \Delta t\end{array} \right.\\ \Rightarrow \left[ {\begin{array}{*{20}{c}}{{p_t}}\\{{v_t}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}1&{\Delta t}\\0&1\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{p_{t - 1}}}\\{{v_{t - 1}}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{\frac{{\Delta {t^2}}}{2}}\\{\Delta t}\end{array}} \right]{a_t}\\ \Rightarrow \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} _t^ - = {F_t}{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_{t - 1}} + {B_t}{a_t}\end{array} $$
可以看到,对于一个线性系统,我们能根据上一时刻状态得到一个简单的估计量,其中F代表了状态转移矩阵,B则代表了控制矩阵,反映了加速度如何作用于当前状态。假设每一时刻的各个维度的不确定性都通过协方差矩阵来描述,另外预测模型本身也不一定准确,所以系统状态的不确定性如下:
$$ \Sigma _t^ - = F\Sigma _{t - 1}^ - {F^T} + Q $$
有了预测值,现在我们通过在路上布设装置来测定小汽车的位置,观测值的误差记为V,然后将真实状态x通过一定变换,可以得到真实状态x和观测状态y的关系:
$$ {y_t} = H{x_t} + V $$
显然,这里的H是[1 0],因为观测到的是位置信息p,同样的我们需要用一个协方差矩阵R来取代上式中的V,以衡量观测不确定性。现在,我们已知此时刻的预测值,观测值,以及几个不确定性矩阵,可以得到此时刻最终的估计:
$$ \begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_t} = {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_t}^ - + {K_t}\left( {{y_t} - H{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} }_t}^ - } \right)\\ {K_t} = \Sigma _t^ - {H^T}{\left( {H\Sigma _t^ - {H^T} + R} \right)^{ - 1}} \end{array} $$
其中 ${y_t} - H{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} _t}^ - $表示实际观测值和预估观测值之间的残差,$K_t$为卡尔曼系数,又叫滤波增益矩阵。可以看到其中同时包含预测状态的协方差矩阵和观测误差矩阵,如果我们相信预测模型多一点,那么对应的协方差矩阵会更小,则K会小一点,反之如果我们相信观测模型多一点,那么K会更大。
最后我们需要更新最有估计值的噪声分布:
$$ {\Sigma _t} = \left( {1 - {K_t}H} \right)\Sigma _t^ - $$
2高斯分布融合
先从高斯分布说起,Kalman滤波算法的假设分布即为高斯分布,而一维的高斯分布概率密度函数及其分布示意图如下:
$$ f\left( {x,\mu ,\sigma } \right) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right] $$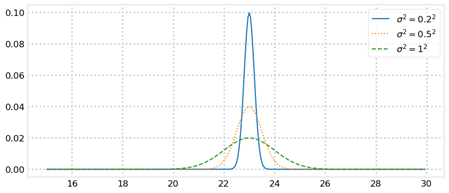
这是一个很简单的高斯分布图,标准差决定分布曲线宽窄,均值决定其中心位置。那么如果我们对任意两个高斯分布进行运算,则会得如下的效果图:
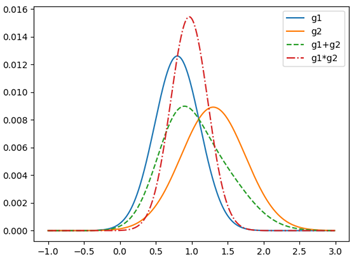
其中两个高斯分布的运算都加入了归一化,可以发现,他们的分布融合也是高斯分布,下面我们对这两个新的高斯分布进行求解证明,主要讲乘法融合,加法以此类推。对于任意两个高斯分布,将二者相乘之后可得:
$$ f\left( {{x_1}} \right)f\left( {{x_2}} \right) = \frac{1}{{{\sigma _1}{\sigma _2}\sqrt {2\pi } }}\exp \left[ { - \left( {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} + \frac{{{{\left( {x - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}} \right)} \right] $$
对于这个概率分布函数,我们利用高斯分布的两个特性进行求解,其一是均值处分布函数取极大值,其二是均值处分布曲线的曲率为其二阶导数,并且与s2成反比。
$$ \begin{array}{l} \because f\left( x \right) = \frac{1}{{{\sigma _1}{\sigma _2}\sqrt {2\pi } }}\exp \left[ { - \left( {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} + \frac{{{{\left( {x - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}} \right)} \right]\\ \therefore f'\left( x \right) = \frac{1}{{{\sigma _1}{\sigma _2}\sqrt {2\pi } }}\exp \left[ { - \left( {\frac{{{{\left( {x - {\mu _1}} \right)}^2}}}{{2{\sigma _1}^2}} + \frac{{{{\left( {x - {\mu _2}} \right)}^2}}}{{2{\sigma _2}^2}}} \right)} \right] * \left[ { - \left( {\frac{{x - {\mu _1}}}{{{\sigma _1}^2}} + \frac{{x - {\mu _2}}}{{{\sigma _2}^2}}} \right)} \right]\\ \because f'\left( \mu \right) = 0\\ \therefore \frac{{\mu - {\mu _1}}}{{{\sigma _1}^2}} + \frac{{\mu - {\mu _2}}}{{{\sigma _2}^2}} = \mu \frac{{{\sigma _1}^2 + {\sigma _2}^2}}{{{\sigma _1}^2{\sigma _2}^2}} - \frac{{{\mu _2}{\sigma _1}^2 + {\mu _1}{\sigma _2}^2}}{{{\sigma _1}^2{\sigma _2}^2}} = 0\\ \therefore \mu = \frac{{{\mu _2}{\sigma _1}^2 + {\mu _1}{\sigma _2}^2}}{{{\sigma _1}^2 + {\sigma _2}^2}}\\ \because f''\left( x \right) = f'\left( x \right) * \left[ { - \left( {\frac{{x - {\mu _1}}}{{{\sigma _1}^2}} + \frac{{x - {\mu _2}}}{{{\sigma _2}^2}}} \right)} \right] - f\left( x \right)\frac{{{\sigma _1}^2 + {\sigma _2}^2}}{{{\sigma _1}^2{\sigma _2}^2}}\\ \therefore f''\left( \mu \right) = - f\left( \mu \right)\frac{{{\sigma _1}^2 + {\sigma _2}^2}}{{{\sigma _1}^2{\sigma _2}^2}}\\ \because f''\left( {{\mu _1}} \right) = - f\left( {{\mu _1}} \right)\frac{1}{{\sigma _1^2}},f''\left( {{\mu _2}} \right) = - f\left( {{\mu _2}} \right)\frac{1}{{\sigma _2^2}}\\ \therefore {\sigma ^2} = \frac{{{\sigma _1}^2{\sigma _2}^2}}{{{\sigma _1}^2 + {\sigma _2}^2}} \end{array} $$
因此我们可以得到如下结论:
$$ \begin{array}{l} f\left( {{x_1}} \right)f\left( {{x_2}} \right) \sim N\left( {\frac{{\sigma _1^2{\mu _2} + \sigma _2^2{\mu _1}}}{{\sigma _1^2 + \sigma _2^2}},\frac{{\sigma _1^2\sigma _2^2}}{{\sigma _1^2 + \sigma _2^2}}} \right)\\ f\left( {{x_1}} \right) + f\left( {{x_2}} \right) \sim N\left( {{\mu _1} + {\mu _2},\sigma _1^2 + \sigma _2^2} \right) \end{array} $$
当然我们遇到的问题大多是多阶的所以要引入多维高斯分布:
$$ \begin{array}{l} f\left( {x,\mu ,\Sigma } \right) = \frac{1}{{\sqrt {{{\left( {2\pi } \right)}^n}\left| \Sigma \right|} }}\exp \left[ { - \frac{1}{2}{{\left( {x - \mu } \right)}^T}{\Sigma ^{ - 1}}\left( {x - \mu } \right)} \right]\\ \Rightarrow {f_1}{f_2} \sim N\left( {{\Sigma _2}{{\left( {{\Sigma _1} + {\Sigma _2}} \right)}^{ - 1}}{\mu _1} + {\Sigma _1}{{\left( {{\Sigma _1} + {\Sigma _2}} \right)}^{ - 1}}{\mu _2},{\Sigma _1}{{\left( {{\Sigma _1} + {\Sigma _2}} \right)}^{ - 1}}{\Sigma _2}} \right) \end{array} $$
3线性卡尔曼滤波
3.1理论推导
首先假设状态变量为x,观测量为z,那么结合贝叶斯后验概率模型:
$$ posterior = \frac{{likelihood \times prior}}{{normalization}} \Leftrightarrow P\left( {\left. x \right|z} \right) = \frac{{P\left( {\left. z \right|x} \right)P\left( x \right)}}{{P\left( z \right)}} $$
多目标跟踪从形式上讲可以理解为最大化后验概率,现在结合第二节的内容,假设状态变量x服从高斯分布,反映的是运动模型的不稳定性。基于状态变量x的估计先验,观测量z也服从高斯分布,反映的是量测误差,比如传感器误差。那么我们就可以利用高斯分布的融合来刻画Kalman滤波器的更新部分。
这里我们先给出一阶Kalman滤波器的公式,其中预测环节就是基于线性运动特性对状态变量的预测,即:
$$ \begin{array}{l} x = Fx + Bu\\ P = FxF^T + Q \end{array} $$
其中$x$为状态变量的均值,$P$为预测方差,那么$Fx$对应的高斯分布方差即为 $FxF^T$ ,而$Q$则是线性运动模型本身的误差,由此得到预测环节。即预测结果服从高斯分布$N(x,P)$。
对于更新环节,同样地,假设量测误差分布满足$N(z,R)$,那么:
$$ \begin{array}{l} \mu = \frac{{{\mu _z}{\sigma _x}^2 + {\mu _x}{\sigma _z}^2}}{{{\sigma _x}^2 + {\sigma _z}^2}} = \frac{{{\sigma _x}^2}}{{{\sigma _x}^2 + {\sigma _z}^2}}{\mu _z} + \frac{{{\sigma _z}^2}}{{{\sigma _x}^2 + {\sigma _z}^2}}{\mu _x}\\ K = \frac{{{\sigma _x}^2}}{{{\sigma _x}^2 + {\sigma _z}^2}}\\ \Rightarrow \mu = K{\mu _z} + \left( {1 - K} \right){\mu _x} = {\mu _x} + K\left( {{\mu _z} - {\mu _x}} \right)\\ \therefore {\sigma ^2} = \frac{{{\sigma _x}^2{\sigma _z}^2}}{{{\sigma _x}^2 + {\sigma _z}^2}} = K{\sigma _z}^2 = \left( {1 - K} \right){\sigma _x}^2 \end{array} $$
代入变量得:
$$ \left\{ \begin{array}{l} K = PH^T/\left( {HPH^T + R} \right)\\ x = Hx + K\left( {z - Hx} \right)\\ P = (1 - KH)P \end{array} \right. $$
上式即为Kalman滤波器是更新环节,其中H是从状态变量到观测量/输出变量的转换矩阵。
3.2实验分析
我们可以看到的是,Kalman滤波器有很多参数,除去运动模型形式假设的F和B参数,存在有多个协方差矩阵P、Q、R。下面我们逐一分析各个参数的影响。
协方差矩阵变化规律
在此之前可以看看不经过更新校正的状态变量均值和方差的变化,假设有如下的运动方式:
$$ \begin{array}{l} \left\{ \begin{array}{l} x = x + \Delta tv\\ v = v \end{array} \right. \Rightarrow \left[ {\begin{array}{*{20}{c}} x\\ v \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ v \end{array}} \right]\\ \Rightarrow P = \left[ {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right]P{\left[ {\begin{array}{*{20}{c}} 1&{\Delta t}\\ 0&1 \end{array}} \right]^T} \end{array} $$
则有状态变量分布如下:
可以看到,在不引入量测的情况下,物体一直保持匀速直线运动,所以其误差的协方差分布一直向水平方向倾斜。
(1)不同Kalman模型
下面我们分别用一阶和二阶的Kalman滤波器去跟踪一个直线运动的物体,其中一阶Kalman滤波完全依赖量测的矫正,二阶Kalman滤波加入了速度因素,可见二阶模型跟踪效果更好,不过其实在这里,如果加入控制变量u,也能恰好达到匀速直线运动的效果。
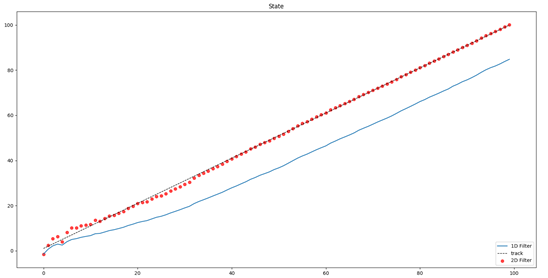
(2) R和Q的影响
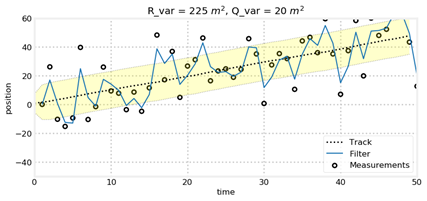
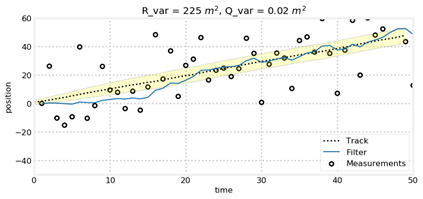
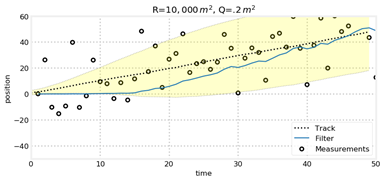
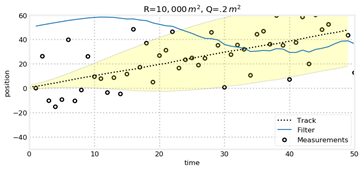
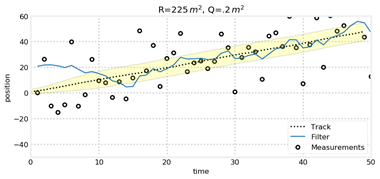
对于匀速直线运动,我们保持量测误差R不变,对比运动估计误差Q发现,Q越小,模型越相信运动规律,而模型正好也是匀速直线运动,因此跟踪效果更好。而当R变大时,模型会更加不相信量测结果,从而使得状态变量的协方差越来越大,但是由于预测环节模型的准确性,跟踪依然比较准确,可以从图中看出,当初始状态偏差很大时,模型不相信量测,导致跟踪轨迹很难与目标轨迹一致,而当R变小却可以重新跟踪到。
(3)P的影响
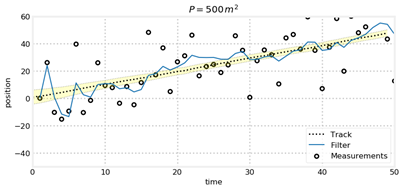
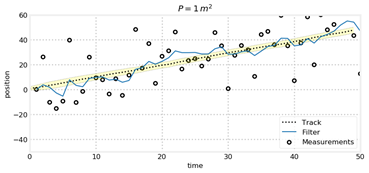
对于上面两幅图,表面上看上去P=1时,跟踪轨迹跟贴近于真实轨迹,但是如果将协方差矩阵P中的参数绘制出来即为:
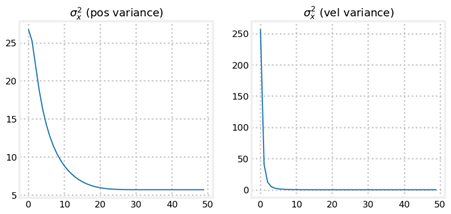
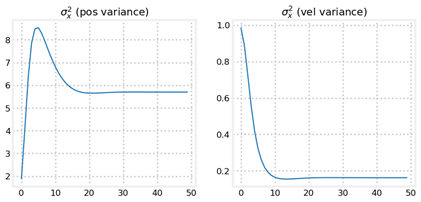
我们可以发现,后者关于位置的方差变化趋势比较复杂,虽然二者均能跟踪到,但是当初始状态估计不好时,P过小会使得跟踪周期变长,而P较大时跟踪效果没有明显降低,因此通常P取值较大。

