前言
Kalman滤波器是多目标跟踪任务中一个经典的运动模型,本次主要以经典应用为主。其中应用算法主要介绍Sort和Deepsort算法。
Sort系列算法的原理不复杂,但是为近些年多目标跟踪的发展提供了很多的实验性baseline帮助,也帮助很多新人入门了。首先我们先谈谈Sort算法,这个算法实际上就是一个很直接的Kalman算法应用。正如我们上一讲所介绍的,Kalman滤波算法需要设计以下几个点:状态量x和观测量z的确定、各个协方差参数(P,Q,R)的确定、运动形式F和转换矩阵H的预设。
1Sort
Sort对于状态量x的设定是一个七维向量:
$$ x = {\left[ {u,v,s,r,\dot u,\dot v,\dot s} \right]^T} $$
分别表示目标中心位置的x,y坐标,相对原始目标框大小的尺度s(可以看做面积尺度)和当前目标框的纵横比,最后三个则是横向,纵向,尺度的变化速率,其中速度部分初始化为0;对于Detection based Tracking框架,由于提供了检测结果,因此相较于Kalman滤波器预测的状态,检测结果就充当了观测量的角色;
各个协方差参数的设定,从Sort提供的代码来看,应该是经验参数:
self.kf.R[2:,2:] *= 10.
self.kf.P[4:,4:] *= 1000.
self.kf.P *= 10.
self.kf.Q[-1,-1] *= 0.01
self.kf.Q[4:,4:] *= 0.01
可以看到,对于Kalman的各个协方差,初始状态为:
$$ \begin{array}{l} P = diag\left( {{{\left[ {\begin{array}{*{20}{c}} {10}&{10}&{10}&{10}&{1e4}&{1e4}&{1e4} \end{array}} \right]}^T}} \right)\\ Q = diag\left( {{{\left[ {\begin{array}{*{20}{c}} 1&1&1&1&{0.01}&{0.01}&{1e{\rm{ - }}4} \end{array}} \right]}^T}} \right)\\ R = diag\left( {{{\left[ {\begin{array}{*{20}{c}} 1&1&{10}&{10} \end{array}} \right]}^T}} \right) \end{array} $$
可以看到,作者主要是基于速度状态不确定性大于位置形状状态不确定性的依据,以及观测行人框的检测位置比形状置信度高的先验;运动形式和转换矩阵的确定,无论是Sort还是Deepsort都是基于匀速运动的假设,即:
$$ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} u\\ v\\ s \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} u\\ v\\ s \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\dot u}\\ {\dot v}\\ {\dot s} \end{array}} \right] \Rightarrow F = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&1&0&0\\ 0&1&0&0&0&1&0\\ 0&0&1&0&0&0&1\\ 0&0&0&1&0&0&0\\ 0&0&0&0&1&0&0\\ 0&0&0&0&0&1&0\\ 0&0&0&0&0&0&1 \end{array}} \right]\\ z = Hx \Rightarrow \left[ {\begin{array}{*{20}{c}} u\\ v\\ s\\ r \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0\\ 0&1&0&0&0&0&0\\ 0&0&1&0&0&0&0\\ 0&0&0&1&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u\\ v\\ s\\ r\\ {\dot u}\\ {\dot v}\\ {\dot s} \end{array}} \right] \end{array} $$然而对于Kalman滤波器的更新环节而言,观测量如何选择也是一个很重要的部分,即对于n条跟踪轨迹而言,如果存在m个观测,如果分配的问题。通常我们采用匈牙利算法/KM算法先对Klaman滤波器预测阶段得到的运动估计和观测进行关联,代价矩阵为二者之间的IOU。匹配成功的则进行Kalman滤波器的更新,匹配失败的跟踪轨迹则视为丢失,匹配失败的观测量则视为新增轨迹;
综上就可以实现各个目标的运动估计和更新。其中对于丢失的轨迹,考虑到跟踪对象或者检测质量的影响,目标经常容易短暂消失,一般情况下我们是允许他参与到后续帧的匹配关联以继续跟踪的。然而Sort跟踪器主要依据的是运动信息,也比较简单,所以实际实现过程中只允许丢失一帧。
2Deepsort
同样地,DeepSort对于Sort算法进行了改进,改进方向有:状态量的调整、协方差参数的调整、代价矩阵的确定方式。
DeepSort对于状态量x的设定是一个八维向量:
$$ x = {\left[ {u,v,\gamma ,h,\dot u,\dot v,\dot \gamma ,\dot h} \right]^T} $$
分别表示目标中心位置的x,y坐标,当前目标框的纵横比和高,以及上述四个状态的速度变量。对于Detection based Tracking框架,由于提供了检测结果,因此相较于Kalman滤波器预测的状态,检测结果就充当了观测量的角色;
各个协方差参数的设定,从DeepSort提供的代码来看,可以看到,对于Kalman的各个协方差,初始状态为:
$$ \left\{ \begin{array}{l} P = diag{\left( {{{\left[ {\begin{array}{*{20}{c}} {2{\sigma _p}h}&{2{\sigma _p}h}&{1e - 2}&{2{\sigma _p}h}&{10{\sigma _v}h}&{10{\sigma _v}h}&{1e - 5}&{10{\sigma _v}h} \end{array}} \right]}^T}} \right)^2}\\ Q = diag{\left( {{{\left[ {\begin{array}{*{20}{c}} {{\sigma _p}h}&{{\sigma _p}h}&{1e - 2}&{{\sigma _p}h}&{{\sigma _v}h}&{{\sigma _v}h}&{1e - 5}&{{\sigma _v}h} \end{array}} \right]}^T}} \right)^2}\\ R = diag{\left( {{{\left[ {\begin{array}{*{20}{c}} {{\sigma _p}h}&{{\sigma _p}h}&{1e - 1}&{{\sigma _p}h} \end{array}} \right]}^T}} \right)^2} \end{array} \right. $$
可以看到,作者引入了位置和速度的标准差这两个额外的参数,整体的设计来看,依旧是速度相对于位置形状不确定性要高,长宽比尽可能变化幅度小。运动形式和转换矩阵的确定,无论是Sort还是Deepsort都是基于匀速运动的假设,不过Deepsort新增了运动的步长即:
$$ \begin{array}{l} F = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{dt}&0&0&0\\ 0&1&0&0&0&{dt}&0&0\\ 0&0&1&0&0&0&{dt}&0\\ 0&0&0&1&0&0&0&{dt}\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right]\\ z = Hx \Rightarrow \left[ {\begin{array}{*{20}{c}} u\\ v\\ \gamma \\ h \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u\\ v\\ \gamma \\ h\\ {\dot u}\\ {\dot v}\\ {\dot \gamma }\\ {\dot h} \end{array}} \right] \end{array} $$对于预测估计和观测量的关联,DeepSort引入了更多的设定,其中IOU的判定作为初筛标准,将不符合要求的关联删除,实际采用的是马氏距离和余弦距离的加权值。其中马氏距离,利用的是Kalman滤波器更新阶段的系统协方差:
$$ {d^{\left( 1 \right)}}\left( {i,j} \right) = {\left( {{d_j} - {y_i}} \right)^T}S_i^{ - 1}\left( {{d_j} - {y_i}} \right) $$
不过马氏距离的取值范围并没有上限,这不利于确定阈值,因此作者巧妙地利用马氏距离和卡方分布的联系,不同维度状态下马氏距离满足95%置信度的阈值如下:| 维度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| :—: | :—-: | :—-: | :—-: | :——: | :——: | :——: | :——: | :——: | :——: |
| 阈值 | 3.842 | 5.992 | 7.815 | 9.4877 | 11.070 | 12.592 | 14.067 | 15.507 | 16.919 |这里实际比对的时候并不会考虑速度状态, 因此只有四维即9.4877。对于表观特征,作者训练了一个Re-ID网络用于特征提取,然后计算余弦距离,最后对两个距离加权。
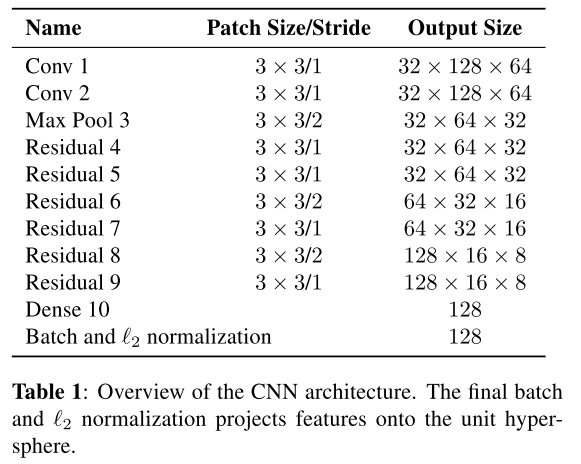
其中作者对于特征向量的处理采用了比较简陋的特征融合方式,即保存轨迹的历史特征,最多100个,每次计算余弦距离之前先将历史特征平均。
最后由于轨迹丢失会暂时保留,因此针对不同时效性的轨迹,采用了级联匹配的方式:

只不过这个看起来可能比较不清楚,CSDN博客有个整理得比较好的:
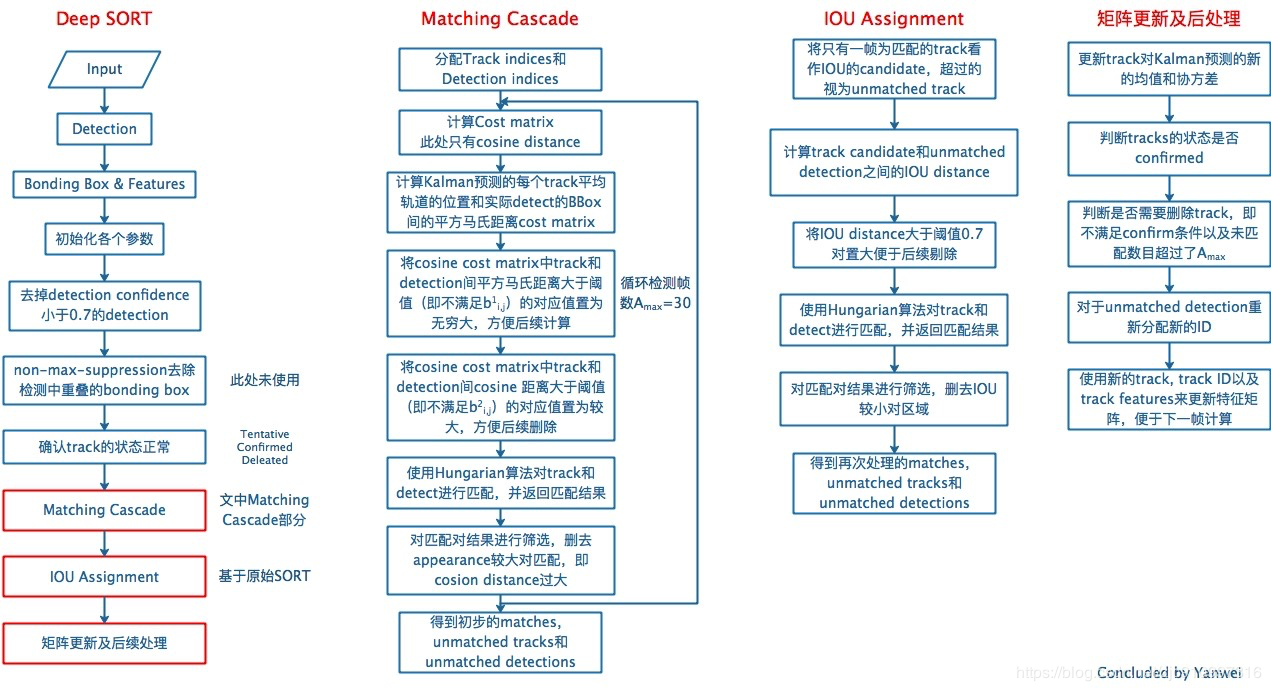
整理而言呢,Sort系列算法原理比较简单,尤其是Sort算法,而Deepsort算法则是开创了Kalman滤波器+Re-ID这种模式的MOT算法先河。两种算法的速度也非常快,不过对于其论文里面所说的SOTA效果,感觉还是有一定的作弊,因为他们采用的是自己训练的Faster RCNN检测器,以及POI检测器。

参考资源
[1]BEWLEY A, GE Z, OTT L, et al. Simple online and realtime tracking[C]. in: 2016 IEEE International Conference on Image Processing (ICIP). IEEE, 2016. 3464-3468.
[2]WOJKE N, BEWLEY A, PAULUS D. Simple online and realtime tracking with a deep association metric[C]. in: 2017 IEEE international conference on image processing (ICIP). IEEE, 2017. 3645-3649.
[3]https://github.com/abewley/sort/blob/master/sort.py
[4]https://github.com/nwojke/deep_sort
[5]https://blog.csdn.net/zjc910997316/article/details/83721573

