前言
无论是机器学习还是最近大热的深度学习算法,很多情况下都需要用到矩阵求导方面的知识,比如拉格朗日乘子法、梯度下降法等等,但是矩阵求导不同于传统的标量求导法则,存在很多冲突。网上以及各种论文中所推导的梯度计算方法,标准都不一样,容易把人搞迷糊。所以我这里理一下矩阵/向量求导相关的原理,并且确定一套属于自己的求导标准,方便自己研究。
1.规则说明
整体来看,矩阵/向量求导涉及到标量,向量和矩阵三者两两之间的求导,那么这其中就涉及到了如下两种规则,这也是众多论文、网站博客让人迷惑的地方:
- 布局(layout):求导后的向量/矩阵形状;
- 链式顺序:比如f(g(x))求导问题中f’(g(x))和g’(x)的顺序排列问题;
- 数据优先级:列优先或者行优先,其中列优先时默认为列向量,对于矩阵的向量展开顺序为逐列展开。
最有意思的地方在于,我们平时所碰见的机器学习和深度学习相关的指标计算,常常会利用范数进行刻画:
$$ \left\{ \begin{array}{l} {\left\| X \right\|_1}{\rm{ = }}{{{\rm{\vec 1}}}^T} \times vec\left( X \right)\\ {\left\| X \right\|_2}{\rm{ = }}tr\left( {{X^T}X} \right)\\ {\left\| X \right\|_\infty }{\rm{ = }}max\left( {\left| X \right|} \right) = {{\vec k}^T} \times vec\left( X \right) \end{array} \right. $$
其中的k向量是一个除了最大值位置处为1,其他位置都为0的矩阵的向量展开。从上面可以看到,如果不考虑函数链式法则(即每次都从结果处开始求导),那么基本上所有的一阶导数问题都能归结为标量对于向量和矩阵的导数问题。但是如果是分段式的求导或者计算二阶导数则需要用到向量和矩阵之间的相互求导。
这里我先确定一些统一规则:
符号说明:标量用小写字母(a,b,c,…)表示,向量用加粗小写字母(x,y,z,w,…)表示,矩阵用加粗的大写字母(A,B,C…)表示;
列优先,即所有向量都是列向量,矩阵的向量化也是逐列展开;
分母布局,即求导后的变量形状与分母对齐,至少保证行数一致,这一点是为了方便待求变量的更新,比如:
$$ \begin{array}{*{20}{l}} {\frac{{\partial y}}{{\partial {\bf{x}}}}}&{ = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial {x_1}}}}\\ {\frac{{\partial y}}{{\partial {x_2}}}}\\ \vdots \\ {\frac{{\partial y}}{{\partial {x_n}}}} \end{array}} \right].}\\ {\frac{{\partial {\bf{y}}}}{{\partial x}}}&{ = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {y_1}}}{{\partial x}}}&{\frac{{\partial {y_2}}}{{\partial x}}}& \cdots &{\frac{{\partial {y_m}}}{{\partial x}}} \end{array}} \right].}\\ {\frac{{\partial {\bf{y}}}}{{\partial {\bf{x}}}}}&{ = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {y_1}}}{{\partial {x_1}}}}&{\frac{{\partial {y_2}}}{{\partial {x_1}}}}& \cdots &{\frac{{\partial {y_m}}}{{\partial {x_1}}}}\\ {\frac{{\partial {y_1}}}{{\partial {x_2}}}}&{\frac{{\partial {y_2}}}{{\partial {x_2}}}}& \cdots &{\frac{{\partial {y_m}}}{{\partial {x_2}}}}\\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial {y_1}}}{{\partial {x_n}}}}&{\frac{{\partial {y_2}}}{{\partial {x_n}}}}& \cdots &{\frac{{\partial {y_m}}}{{\partial {x_n}}}} \end{array}} \right].}\\ {\frac{{\partial y}}{{\partial {\bf{X}}}}}&{ = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial {x_{11}}}}}&{\frac{{\partial y}}{{\partial {x_{12}}}}}& \cdots &{\frac{{\partial y}}{{\partial {x_{1q}}}}}\\ {\frac{{\partial y}}{{\partial {x_{21}}}}}&{\frac{{\partial y}}{{\partial {x_{22}}}}}& \cdots &{\frac{{\partial y}}{{\partial {x_{2q}}}}}\\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial y}}{{\partial {x_{p1}}}}}&{\frac{{\partial y}}{{\partial {x_{p2}}}}}& \cdots &{\frac{{\partial y}}{{\partial {x_{pq}}}}} \end{array}} \right].} \end{array} $$
可以看到上面两个向量之间的求导得到的是一个矩阵,这个是符合求导规则的,但是机器学习中的参数更新我们会利用梯度进行更新,这一点会在以后讲解梯度下降法、牛顿法、共轭梯度下降法的时候介绍。既然要更新,则肯定需要保证导数和参数形状一模一样,那么我们根据梯度的累加性得到:
$$ \vec x = \vec x - \eta \frac{{\partial \vec y}}{{\partial \vec x}} \times \vec 1 $$
这样做还有一个好处,那就是待求参数的转置不影响求导结果,即:
$$ \frac{{\partial \left( {Ax} \right)}}{{\partial x}} = \frac{{\partial \left( {{x^T}{A^T}} \right)}}{{\partial x}}={A^T} $$
链式法则和运算法则对于分子的组成很敏感,如果详细推导会很麻烦,当分子为标量时,可以用第2章的内容进行推导,当分子为向量时,有如下规律:
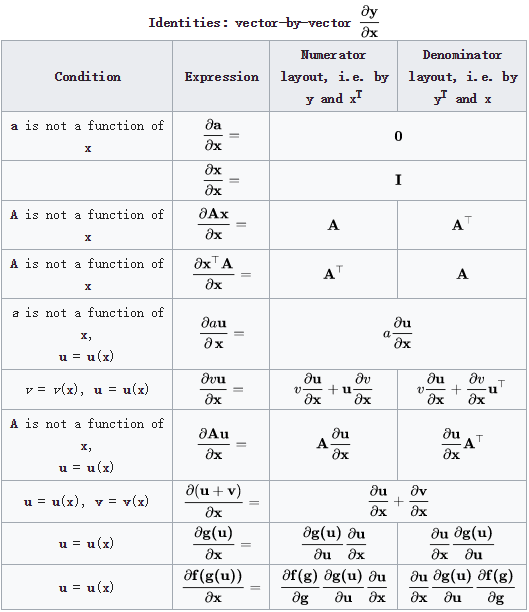
2.矩阵求导
2.1 迹的引入
上面所介绍的是标量和向量相关的求导法则,但是涉及到矩阵问题的时候,会出现不一样的地方。由于向量或者矩阵求导的本质是相应元素标量之间的求导,所以对于一个m x n的矩阵A和p x q的矩阵B之间导数,必定是一个mp x nq的大型矩阵,这个操作利用简单Hadamard矩阵乘法是做不到的,我们也无法利用上面的规则。所以对于这类问题可以利用方阵的迹进行求解,其中标量也可以视为是1 x 1大小的方阵,下面所介绍的规则同样适用于标量对向量的求导。
首先我们来研究一下一元微积分和多元微积分微分的原始定义:
$$ \left\{ \begin{array}{l} df = f'\left( x \right)dx\\ df = \sum\limits_{i = 1}^n {\frac{{\partial f}}{{\partial {x_i}}}d{x_i}} \end{array} \right. \Rightarrow df = {\left( {\frac{{\partial f}}{{\partial x}}} \right)^T}dx $$
可以发现可以用导数的转置向量与微分向量的内积来表示导数,所以矩阵的微分也可以定义为:
$$ df = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{\partial f}}{{\partial {X_{ij}}}}} } d{X_{ij}} = tr\left( {{{\frac{{\partial f}}{{\partial X}}}^T}dX} \right) $$
,其中tr表示矩阵的迹,即矩阵对角线元素之和。不同于上面的求导法则,下面我们针对分子为标量或者方阵的矩阵/向量求导设置新的运算法则:
- 微分法则,其中$\odot$表示矩阵点乘,$\sigma$表示元素级函数:
$$ \left\{ {\begin{array}{*{20}{l}} {d\left( {X \pm Y} \right) = dX \pm dY}\\ \begin{array}{l} d\left( {XY} \right) = \left( {dX} \right)Y + XdY\\ d\left( {X \odot Y} \right) = dX \odot Y + X \odot dY\\ d\left( {\sigma \left( X \right)} \right) = \sigma '\left( X \right) \odot dX \end{array} \end{array}} \right. $$
微分与迹:
$$ \left\{ \begin{array}{l} d\left( {tr(X)} \right) = tr\left( {dX} \right)\\ dx = tr\left( {dx} \right)\\ d\left( {{X^T}} \right) = {\left( {dX} \right)^T}\\ tr\left( {{X^T}} \right) = tr\left( X \right) \end{array} \right. $$迹的运算法则:
$$ \left\{ \begin{array}{l} tr\left( {A \pm B} \right) = tr\left( A \right) \pm tr\left( B \right)\\ tr\left( {ABC} \right) = tr\left( {CAB} \right) = tr\left( {BCA} \right)\\ tr\left( {{A^T}\left( {B \odot C} \right)} \right) = tr\left( {{{\left( {A \odot B} \right)}^T}C} \right) \end{array} \right. $$
其中第二项并不是说矩阵的迹具有交换律,而是轮换不变性,即向左向右移位。特殊运算:
$$ \left\{ \begin{array}{l} d\left( {X{X^{ - 1}}} \right) = dX{X^{ - 1}} + Xd{X^{ - 1}} = dI = 0 \Rightarrow d{X^{ - 1}} = - {X^{ - 1}}dX{X^{ - 1}}\\ d\left| X \right| = tr\left( {{X_{adj}}dX} \right)\mathop \to \limits^{inversable} \left| X \right|tr\left( {{X^{ - 1}}dX} \right) \end{array} \right. $$
2.2 算例说明
由于绝大部分机器学习算法中涉及到的求导都是标量对向量和矩阵的,所以这里用迹来求解非常方便,我们还是保证列优先:
eg1: 假设
y=AXB是标量,那么其关于X的导数为:
$$ \begin{array}{l} dy = tr\left( {dy} \right)\\ = tr\left( {d\left( {AXB} \right)} \right)\\ = tr\left( {dAXB + AdXB + AXdB} \right)\\ = tr\left( {AdXB} \right)\\ = tr\left( {BAdX} \right)\\ = tr\left( {{{\left( {{A^T}{B^T}} \right)}^T}dX} \right)\\ \Rightarrow \frac{{\partial y}}{{\partial X}} = {\left( {{A^T}{B^T}} \right)^T} \end{array} $$eg2:
$$ \begin{array}{l} f = tr\left( {{Y^T}MY} \right),Y = \sigma \left( {WX} \right)\\ \Rightarrow df\\ = tr\left( {d{Y^T}MY + {Y^T}MdY} \right)\\ = tr\left( {{Y^T}{M^T}dY + {Y^T}MdY} \right)\\ = tr\left( {{Y^T}\left( {{M^T} + M} \right)dY} \right)\\ \Rightarrow \frac{{\partial f}}{{\partial Y}} = \left( {M + {M^T}} \right)Y\\ \because dY = \sigma '\left( {WX} \right) \odot \left( {WdX} \right)\\ \therefore df = tr\left( {{{\frac{{\partial f}}{{\partial Y}}}^T}dY} \right)\\ = tr\left( {{{\frac{{\partial f}}{{\partial Y}}}^T}\left( {\sigma '\left( {WX} \right) \odot \left( {WdX} \right)} \right)} \right)\\ = tr\left( {\left( {{{\frac{{\partial f}}{{\partial Y}}}^T} \odot \sigma '\left( {WX} \right)} \right)WdX} \right)\\ \Rightarrow \frac{{\partial f}}{{\partial X}} = {W^T}\left( {\frac{{\partial f}}{{\partial Y}} \odot \sigma '{{\left( {WX} \right)}^T}} \right) \end{array} $$eg3: 岭回归模型,
X为m x n的矩阵,w为n x 1的向量,y为m x 1的向量
$$ \begin{array}{l} l = {\left\| {Xw - y} \right\|^2} + \lambda \left\| w \right\|\\ = {\left( {Xw - y} \right)^T}\left( {Xw - y} \right) + {w^T}w\\ \Rightarrow dl = tr\left( {dl} \right)\\ = tr\left( {d{{\left( {Xw - y} \right)}^T}\left( {Xw - y} \right) + {{\left( {Xw - y} \right)}^T}d\left( {Xw - y} \right) + d{w^T}w + {w^T}dw} \right)\\ \because d\left( {Xw} \right) = dXw + Xdw = Xdw\\ \therefore dl = tr\left( {{{\left( {Xdw} \right)}^T}\left( {Xw - y} \right) + {{\left( {Xw - y} \right)}^T}Xdw + {w^T}dw + {w^T}dw} \right)\\ = tr\left( {2{{\left( {Xw - y} \right)}^T}Xdw + 2{w^T}dw} \right)\\ = tr\left( {2{{\left( {{X^T}\left( {Xw - y} \right)} \right)}^T}dw + 2{w^T}dw} \right)\\ \therefore \frac{{\partial l}}{{\partial w}} = 2\left( {{X^T}\left( {Xw - y} \right) + w} \right) = 0\\ \therefore \left( {{X^T}X + I} \right)w = {X^T}y\\ \therefore w = {\left( {{X^T}X + I} \right)^{ - 1}}{X^T}y \end{array} $$eg4: 神经网络(交叉熵损失函数+softmax激活函数+2层神经网络),
y是一个除一个元素为1之外,其他元素都为0的m x 1向量,W2为m x p矩阵,W1为p x n矩阵,x是n x 1向量:
$$ \begin{array}{l} l = - {y^T}\log softmax\left( {{W_2}\sigma \left( {{W_1}x} \right)} \right)\\ \Rightarrow \left\{ \begin{array}{l} l = - {y^T}\log {h_2}\\ {h_2} = softmax\left( {{a_2}} \right) = \frac{{{e^{{a_2}}}}}{{{{\vec 1}^T}{e^{{a_2}}}}}\\ {a_2} = {W_2}{h_1}\\ {h_1} = \sigma \left( {{a_1}} \right) = \frac{1}{{1 + {e^{ - {a_1}}}}}\\ {a_1} = {W_1}x \end{array} \right.\\ \therefore dl = tr\left( {dl} \right) = tr\left( { - {y^T}\left( {\frac{1}{{{h_2}}} \odot d{h_2}} \right)} \right)\\ \left( 1 \right)if\;i = j\\ \frac{{\partial softmax\left( {a_{_2}^i} \right)}}{{\partial a_{_2}^j}} = \left( {\frac{{{e^{a_{_2}^i}}}}{{k + {e^{a_{_2}^i}}}}} \right)'\\ = \left( {1 - \frac{k}{{k + {e^{a_{_2}^i}}}}} \right)'\\ = \frac{{k{e^{a_{_2}^i}}}}{{{{\left( {k + {e^{a_{_2}^i}}} \right)}^2}}}\\ = \frac{{{e^{a_{_2}^i}}}}{{k + {e^{a_{_2}^i}}}}\frac{k}{{k + {e^{a_{_2}^i}}}}\\ = softmax\left( {a_{_2}^i} \right)\left( {1 - softmax\left( {a_{_2}^i} \right)} \right)\\ = h_2^i\left( {1 - h_2^i} \right)\\ \left( 2 \right)if\;i \ne j:\\ \frac{{\partial softmax\left( {a_{_2}^i} \right)}}{{\partial a_{_2}^j}} = \left( {\frac{{{e^{a_{_2}^i}}}}{{n + {e^{a_{_2}^j}}}}} \right)'\\ = \left( { - \frac{{{e^{a_{_2}^i}}{e^{a_{_2}^j}}}}{{n + {e^{a_{_2}^j}}}}} \right)\\ = - \frac{{{e^{a_{_2}^i}}{e^{a_{_2}^j}}}}{{{{\left( {n + {e^{a_{_2}^j}}} \right)}^2}}}\\ = - h_2^ih_2^j\\ \therefore 利用向量对向量求导的定义可得:\\ \therefore d{h_2} = (diag\left( {{h_2}} \right) - {h_2}h_2^T)d{a_2}\\ dl = tr\left( { - {y^T}\left( {\frac{1}{{{h_2}}} \odot \left( {diag\left( {{h_2}} \right) - {h_2}h_2^T} \right)d{a_2}} \right)} \right)\\ = tr\left( { - {{\left( {y \odot \frac{1}{{{h_2}}}} \right)}^T}\left( {diag\left( {{h_2}} \right) - {h_2}h_2^T} \right)d{a_2}} \right)\\ = tr\left( {\left( { - {y^T} + h_2^T} \right)d{a_2}} \right)\\ = tr\left( {{{\left( {{h_2} - y} \right)}^T}d{a_2}} \right)\\ \because d{a_2} = d{W_2}{h_1} = {W_2}d{h_1}\\ \therefore dl = tr\left( {{{\left( {{h_2} - y} \right)}^T}d{W_2}{h_1}} \right) = tr\left( {{h_1}{{\left( {{h_2} - y} \right)}^T}d{W_2}} \right)\\ \Rightarrow \frac{{\partial l}}{{\partial {W_2}}} = \left( {{h_2} - y} \right)h_1^T\\ \because d{h_1} = \sigma '\left( {{a_1}} \right) \odot d{a_1} = {h_1} \odot \left( {1 - {h_1}} \right) \odot d{a_1}\\ d{a_1} = d{W_1}x\\ \therefore dl = tr\left( {{{\left( {{h_2} - y} \right)}^T}{W_2}\left( {{h_1} \odot \left( {1 - {h_1}} \right) \odot d{W_1}x} \right)} \right)\\ = tr\left( {{{\left( {{W_2}^T\left( {{h_2} - y} \right) \odot {h_1} \odot \left( {1 - {h_1}} \right)} \right)}^T}d{W_1}x} \right)\\ = tr\left( {x{{\left( {{W_2}^T\left( {{h_2} - y} \right) \odot {h_1} \odot \left( {1 - {h_1}} \right)} \right)}^T}d{W_1}} \right)\\ \Rightarrow \frac{{\partial l}}{{\partial {W_1}}} = \left( {{W_2}^T\left( {{h_2} - y} \right) \odot {h_1} \odot \left( {1 - {h_1}} \right)} \right){x^T} \end{array} $$
这里主要是为了强调这个过程,实际上log和softmax在一起时,可以将乘除法转化为加减法。
2.3 矩阵拓展
上面只介绍了向量与标量、向量与向量和矩阵与标量的求导规则,但是对于矩阵与矩阵和矩阵与向量的求导尚未说明,这里只简单说明。
我们在之前讨论过,矩阵求导本质上是矩阵对矩阵每一个元素的求导,那么为了更方便整体求导,不妨先将矩阵转化为向量,即将矩阵拉伸为列向量,然后再求导,其同样满足:
$$ \begin{array}{l} vec\left( {dF} \right) = {\frac{{\partial F}}{{\partial X}}^T}vec\left( {dX} \right)\\ \left\{ \begin{array}{l} vec\left( {AXB} \right) = \left( {{B^T} \otimes A} \right)vec\left( X \right)\\ vec\left( {{A^T}} \right) = {K_{mn}}vec\left( A \right)\\ vec\left( {A \odot X} \right) = diag\left( A \right)vec\left( X \right) \end{array} \right. \end{array} $$
其中$\otimes$表示Kronecker积,${K_{mn}}$表示转换矩阵,其实就是转换前后的仿射矩阵,关于这两个算子有如下规律:
$$ \left\{ \begin{array}{l} {\left( {A \otimes B} \right)^T} = {A^T} \otimes {B^T}\\ vec\left( {a{b^T}} \right) = b \otimes a\\ \left( {A \otimes B} \right)\left( {C \otimes D} \right) = \left( {AC} \right) \otimes \left( {BD} \right)\\ {K_{mn}} = K_{nm}^T\\ {K_{mn}}K_{nm}^T = I\\ {K_{pm}}\left( {A \otimes B} \right){K_{nq}} = B \otimes A \end{array} \right. $$
如果想利用上面的方式求导,在参数更新的时候,比如AXB,其中A(m x n),X(n x p),B(p x q),需要对导数(pn x qm)乘以一个qm x 1的全1向量,用来将梯度累加,然后重塑为矩阵n x p。

