前言
随着这两年GNN的发展,其对于关系的建模特性也被引入了多目标跟踪领域,这次我通过对这两年基于GNN的MOT算法的介绍来分析其特点。相关MOT和数据关联的基础知识可以去我的专栏查看。
1.EDA_GNN
论文题目: Graph Neural Based End-to-end Data Association Framework for Online Multiple-Object Tracking
作者:Xiaolong Jiang, Peizhao Li, Yanjing Li, Xiantong Zhen
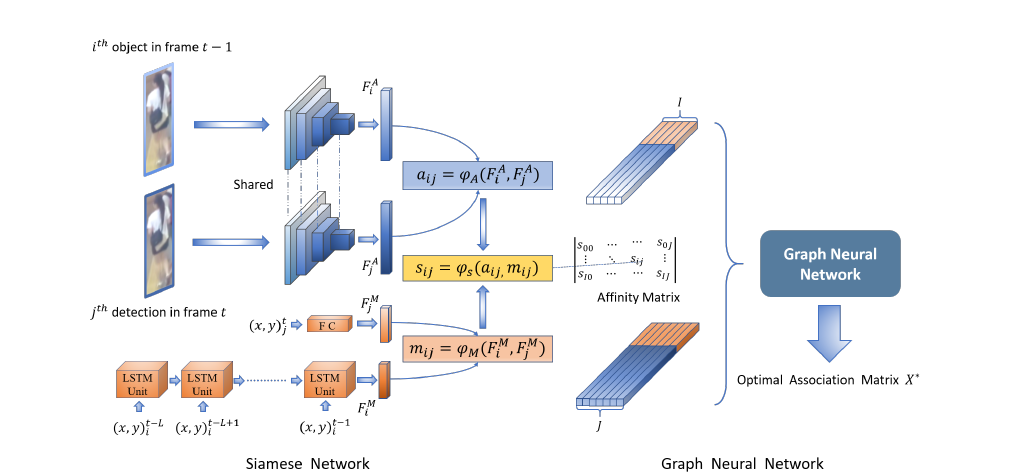
从算法的示意图可以看到,作者通过一个孪生网络求得了观测目标j与当前目标轨迹i的表观相似度,然后取目标轨迹的历史位置为输入,通过LSTM得到预测的位置,计算该位置与观测目标位置的运动相似度,两个相似度结合构建相似度矩阵。至此,所有目标轨迹与观测目标的相似度构成了一个二部图,以目标和观测信息作为节点,相似度作为边权,表观特征和位置信息拼接作为节点属性特征。
然后基于消息传递机制,作者通过GNN的网络框架实现对节点特征的更新:
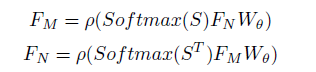
邻接矩阵的normalization采用的是row-wise softmax,即对相似度矩阵进行逐行softmax,可以用注意力的方式来理解,W为待学习的权重。最后通过一个激活函数ReLU实现特征的更新。对于边权关系的更新则是简单地利用MLP将两个节点特征的差转换为标量。
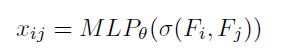
在训练的时候,损失函数由三部分组成:
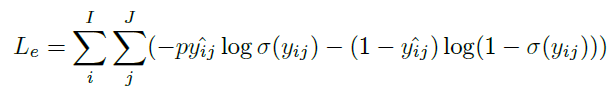
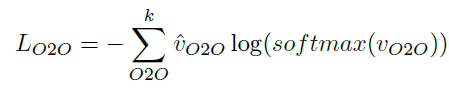

其中第一部分是预测得到的关联矩阵的分类损失,第二部分则是将groundtruth中的关联对取出,计算分类损失,第三部分是将新出/消失的目标单独取出,计算MSE损失。
2.DAN
论文题目: Deep association: End-to-end graph-based learning for multiple object tracking with conv-graph neural network
作者:Cong Ma, Yuan Li, Fan Yang, Ziwei Zhang, Yueqing Zhuang, Huizhu Jia, Xiaodong Xie
备注信息:ICMR2019
这里的DAN并非我之前提过的DAN,其整理流程跟EDA_GNN基本一样:
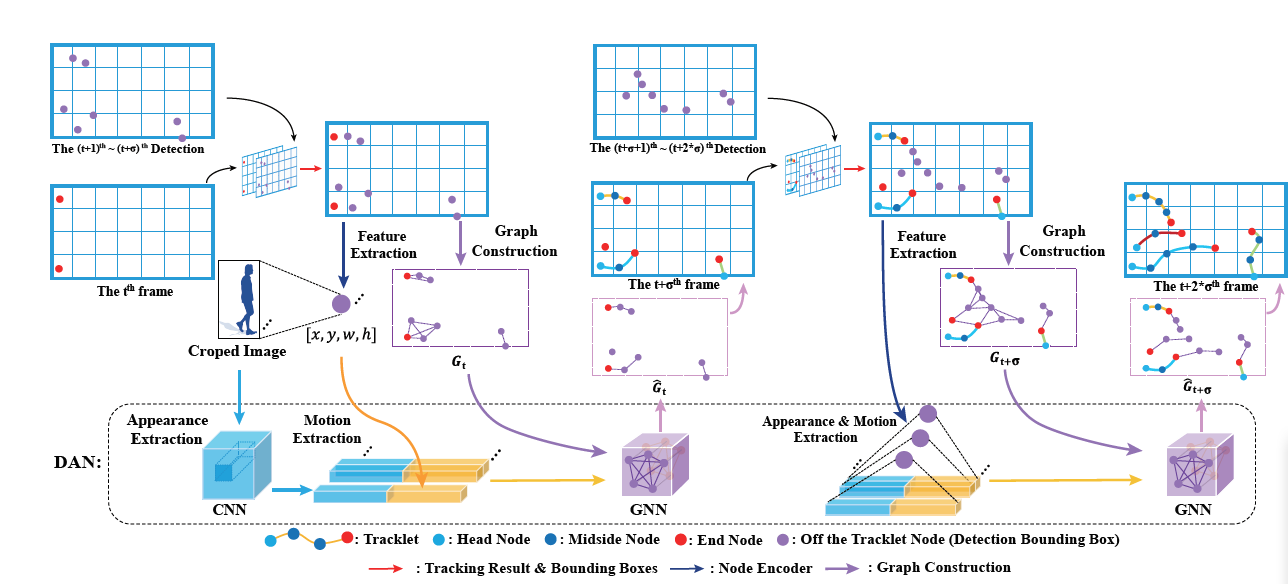
都是先提取表观和运动特征,由此构建网络图,通过GNN得到最终的关联矩阵。首先相似度矩阵怎这里用的是IOU信息:
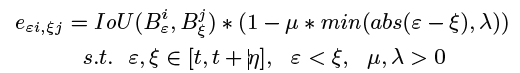
IOU后面的部分是帧间差,如果目标存在跨帧链接,那么间隔越久,相似度越低。不过DAN与EDA_GNN不同的是,并没有将图结构构建为二部图,而是将跟踪节点和观测节点统一为节点集合,因此邻接矩阵/相似度矩阵就变成了(m+n)x(m+N),这就是最基础的GNN网络结构了。所以节点特征的更新就是:
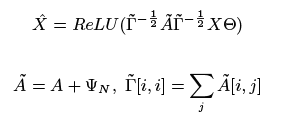
邻接矩阵的更新为:
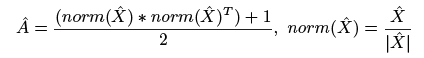
损失函数为Graph Loss,即对正负链接边权的交叉熵损失函数:
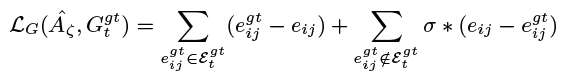
结果如下:

3.GNMOT
论文题目:Graph Networks for Multiple Object Tracking
作者:Jiahe Li, Xu Gao, Tingting Jiang
备注信息:WACV2020
论文链接:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9093347
首先我们看看算法流程:
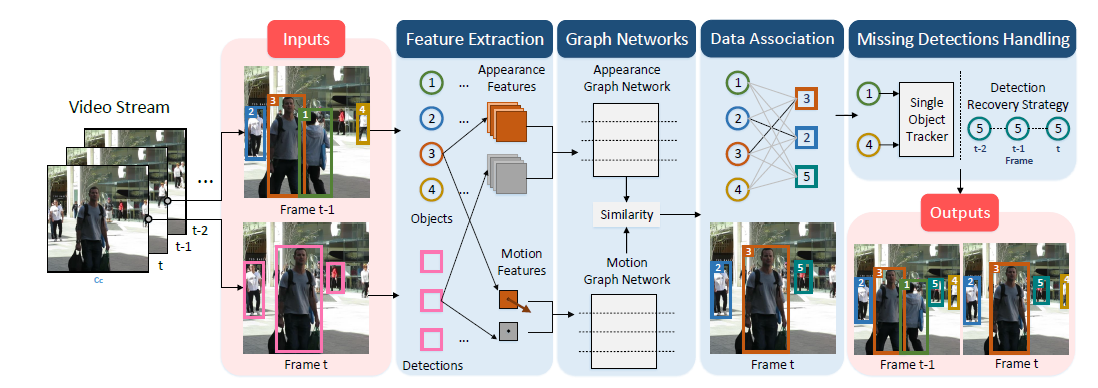
可以看到,GNMOT的不同在于表观和运动部分分别采用了GNN网络,二者结合得到的是相似度矩阵,由此输入数据关联部分。关于GNN网络的更新流程,作者设计了4步:
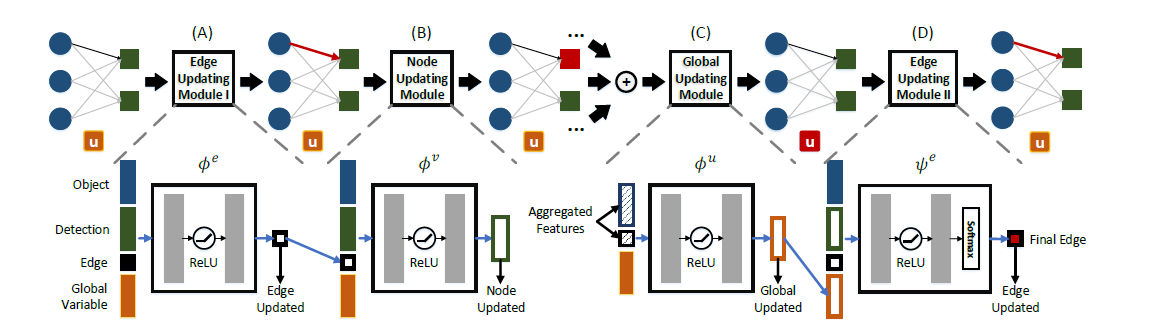
其中第一次边和节点的更新都是通过两层FC进行更新的。第三次的全局更新这里,作者引入了一个全局变量u,先计算所有节点的特征均值和边权均值,再通过两层FC进行更新。这里的u会在出现在所有更新过程中,作为一个调节量。
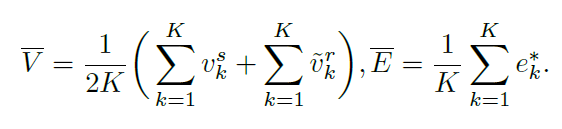
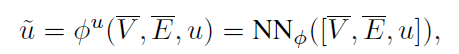
最后一次的边权更新则是在两层FC之后再加了一层softmax层。
4.MPN Tracker
论文题目:Learning a Neural Solver for Multiple Object Tracking
作者:Brasó G, Leal-Taixé L
备注信息:CVPR2020
论文链接:https://arxiv.org/abs/1912.07515
代码链接:https://github.com/selflein/GraphNN-Multi-Object-Tracking
我之前也介绍过这篇文章,但是之前不懂GNN,所以只能做搬运工,现在学习了GNN,所以就再次分析一下。首先是图的构建,图节点由所有帧的所有目标构成,直接将观测信息作为节点,没有跟踪,只有关联。节点属性特征由训练得到的表观特征和几何特征构成,其中几何特征为位置和形状。并且定义表观特征距离用欧氏距离度量,几何特征距离用下面的公式度量:
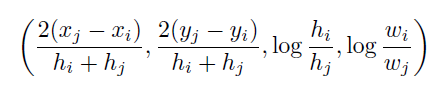
时间特征自然就是帧数,这几个特征通过一个MLP网络得到最终的特征表达。
边的连接自然就是跨帧节点存在连接,而同一帧节点不存在连接,边权的设定就是上面的距离度量。也就是说,这相当于一个端到端的离线跟踪框架。
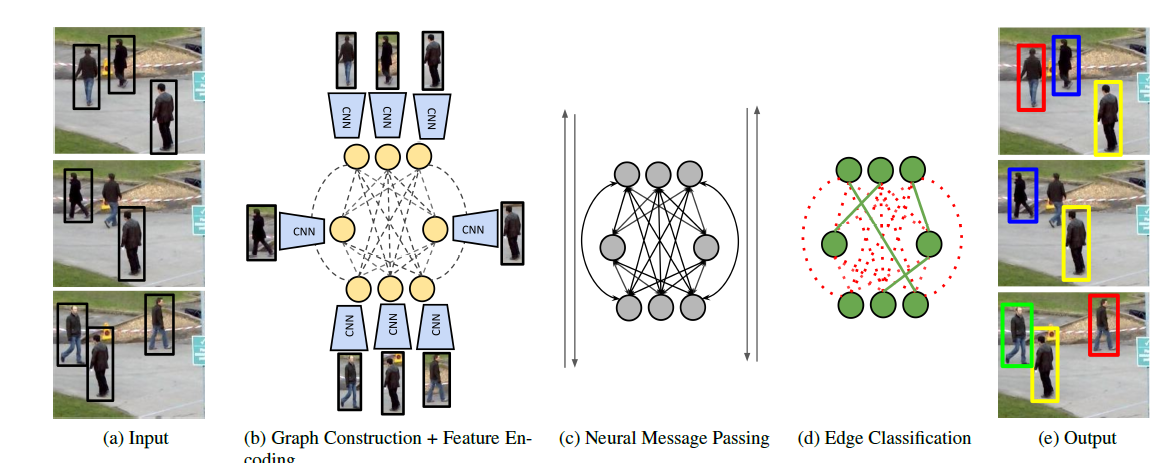
消息传递机制中,对于边权的更新和节点的更新方式如下:
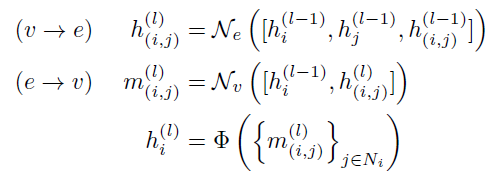
其中对于边的更新就是由节点特征和原始边权通过MLP过程更新的。对于节点的更新,由于一个节点连接有多条边,所以需要进行聚合,聚合方式可以求和、取平均,还可以是取最大值。而更新的代数L自然也就决定了图卷积网络的感受野,当L越大时,与之相关的节点在时间跨度上越大。
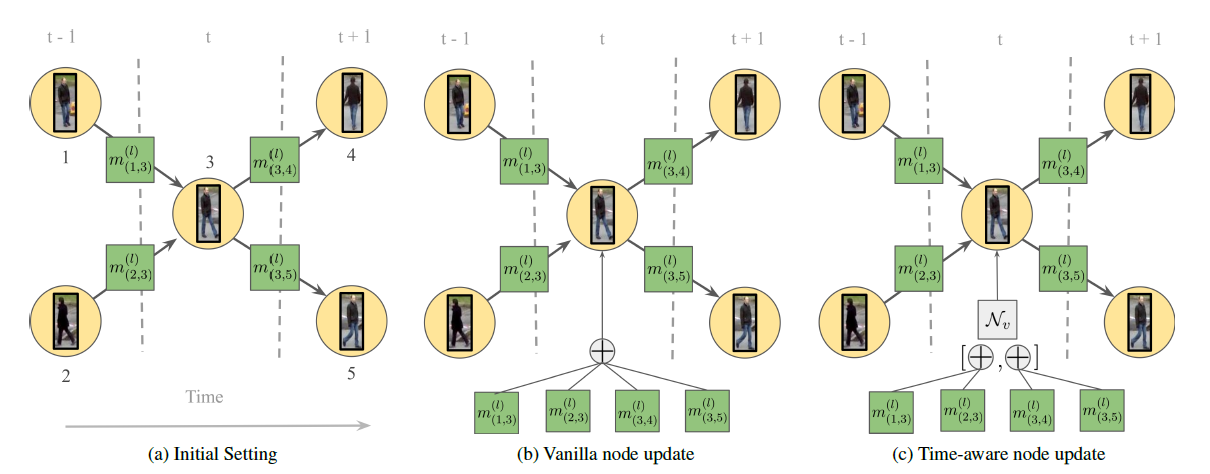
上面这个图从左往右是不同时间帧的节点,这里举的例子是一个相邻三帧的节点连接。原始的更新机制中,对于节点的更新会将周围边的影响通过求和的方式聚合。而这里作者考虑了时间因素,将时间分为了过去和未来两个部分:
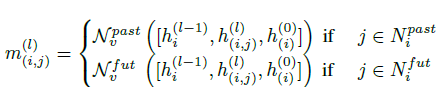
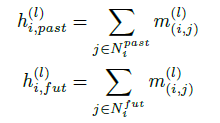

然后通过拼接的方式聚合,最后利用MLP结构实现特征降维。
可以看下消息传递代数的影响:
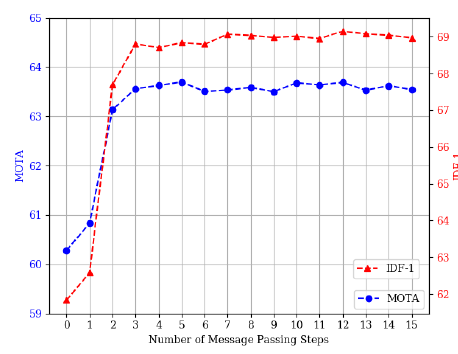
我们发现在3代的时候就已经达到了性能上限,不过为了保证鲁棒性,作者还是选了12.
不得不说离线的方法在IDF1指标上的表现很好:
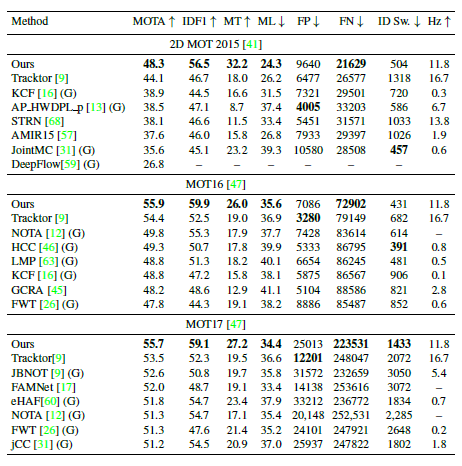
PS:大家可能对于第一张图中的Edge Classification有疑惑,即如何实现的边的稀疏化。这里由于每条边权都经过了一个sigmoid层,因此作者直接利用固定阈值0.5进行了裁剪。
5.GNN3DMOT
论文题目:Graph Neural Network for 3D Multi-Object Tracking with Multi-Feature Learning
作者:Xinshuo Weng, Yongxin Wang, Yunze Man, Kris Kitani
备注信息:CVPR2020
从这篇开始,接下来的全是这个组的文章。这篇文章所涉及的算法框架很完整,值得一读:
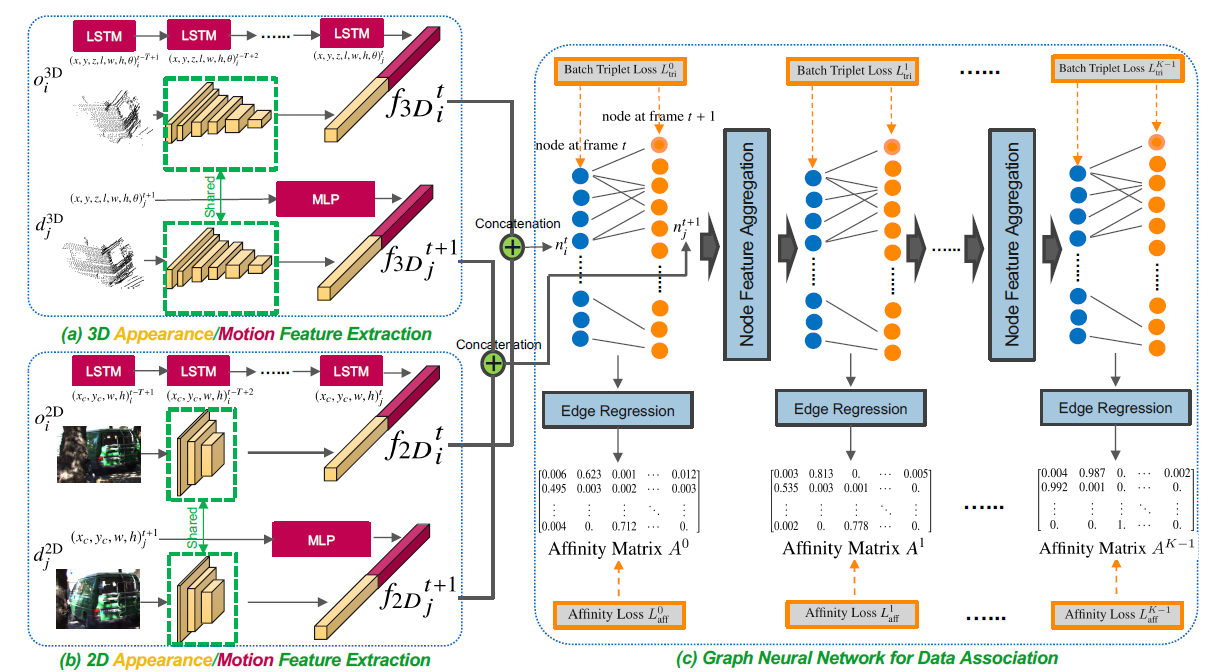
算法流程通过这张图可以很容易得到,运动特征是通过LSTM网络回归得到的,表观特征是通过CNN网络得到的,二者相拼接。其中3D部分的输入则是点云信息和3D位置信息,o表示物体,d表示检测。将2D和3D特征拼接/相加得到每个节点的特征。而节点自然就是上一帧存在的目标和当前帧的观测。
对于边权/相似度矩阵的确定,作者尝试了三种方式,余弦距离、欧氏距离还有网络回归,即上图中的Edge Regression:
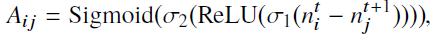
当然这个也是边权更新的机制,而对于节点 消息传递机制,作者也设计了四种:
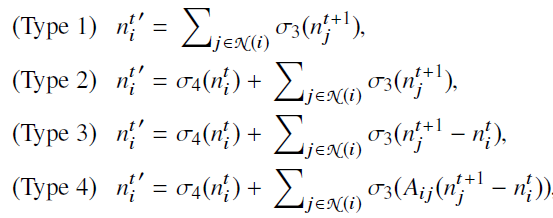
方法很明了,我就不细讲了,可以看到聚合方式都是求和。另外由算法框架示意图可知,每次消息传递都会计算关联矩阵的损失,那么为什么会采用batch triplet loss呢?
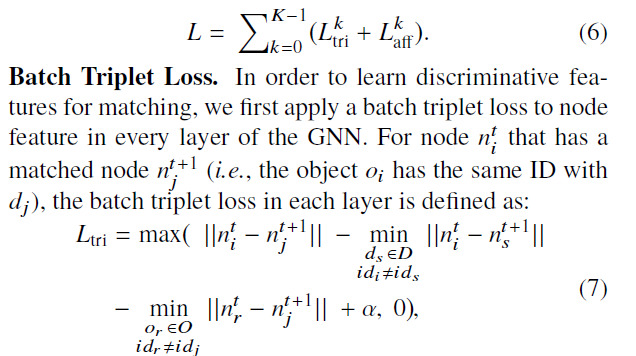
作者把关联矩阵中的每条边权看作了N对匹配,三元组损失中,首先选取相邻帧中的一对连接i,j,然后分别选取不同id的两帧节点r,s,计算上述损失。即要保证不同帧间不同id身份的边权的最小距离越大越好。而对于相似度损失,则是采用了两种交叉熵损失:
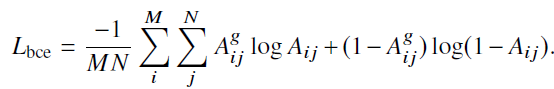
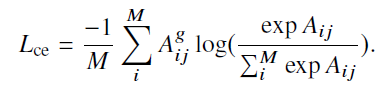
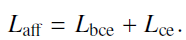
效果如下:
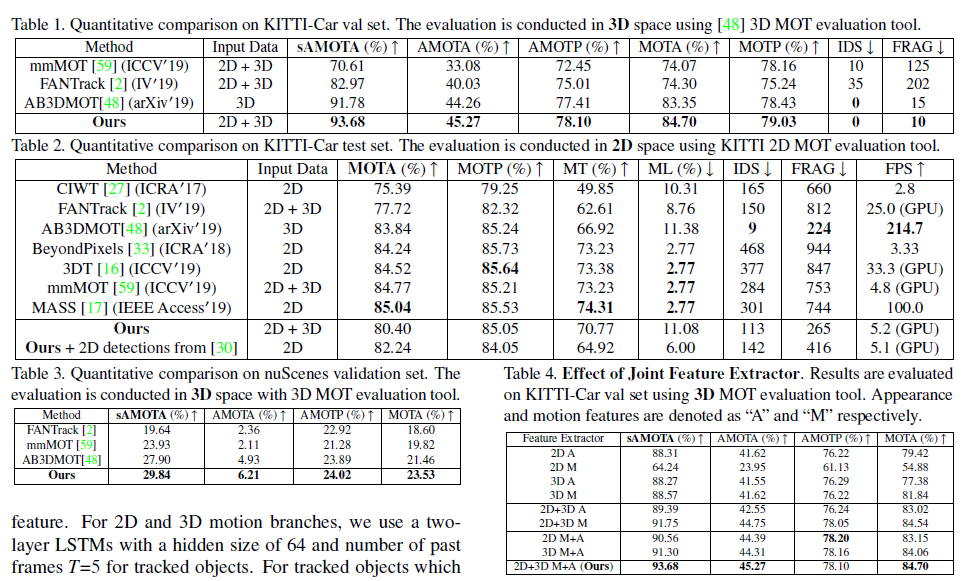
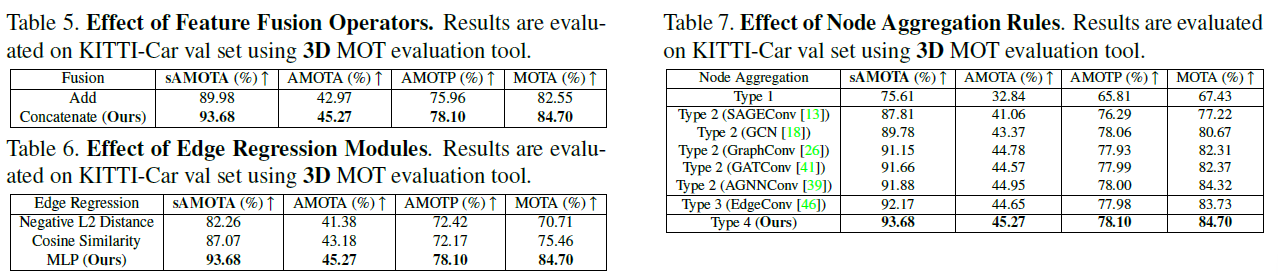
可以看到利用网络回归的方式得到的相似度度量方式要比余弦距离和欧氏距离好,2D和3D特征融合的方式更优,结合了关联矩阵和节点差异的聚合方式,即Table7中的type4更优。
6.GNNTrkForecast
论文题目:Joint 3D Tracking and Forecasting with Graph Neural Network and Diversity Sampling
作者:Xinshuo Weng, Ye Yuan, and Kris Kitani
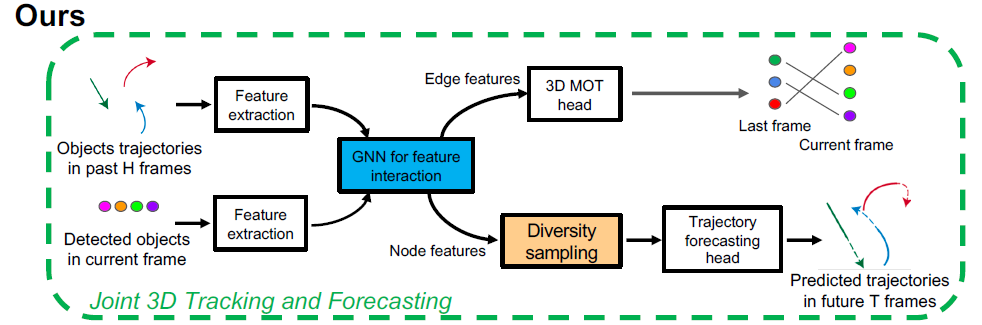
这篇论文里面,作者通过GNN将3D MOT和轨迹预测结合在一起了。其中对于GNN网络的构建以及关联矩阵的获取跟之前的论文几乎一致,具体我们就不介绍了:
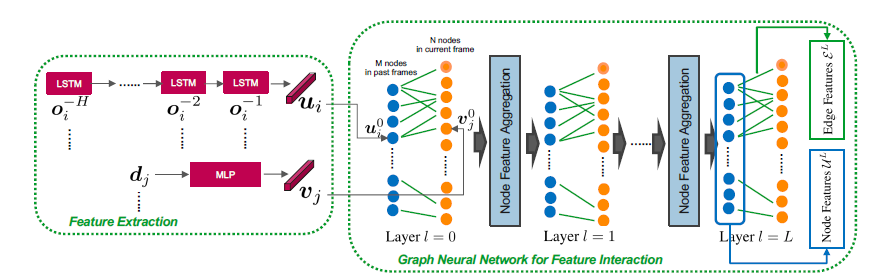
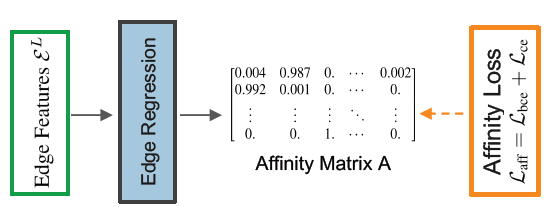
那么3D MOT分支实际上就是GNN模型中的一部分,是根据GNN的边权矩阵进行数据关联:
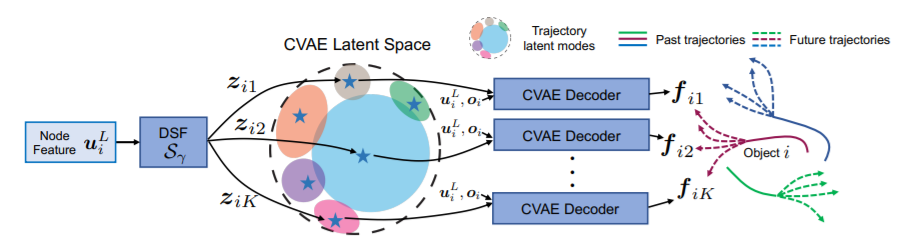
而对于轨迹预测分支,作者基于条件自编码器的形式,设计的流程图如下,由于这块我不熟悉,所以我就不细讲了。
效果如下:

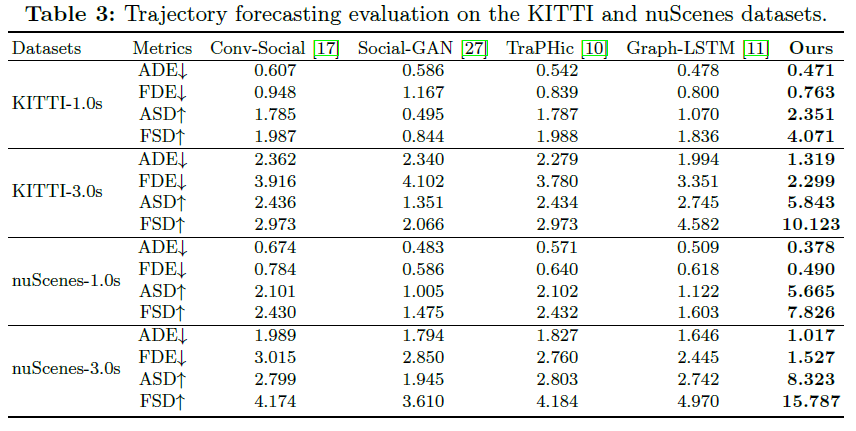
7. JDMOT_GNN
论文题目:Joint Detection and Multi-Object Tracking with Graph Neural Networks
作者:Yongxin Wang,Xinshuo Weng,and Kris Kitani
也许是看到最近联合检测和跟踪的框架很热门,作者团队又给加入了GNN模块,所以我们简单提一下:

最开始的表观和运动特征部分就不提了,一个是LSTM/MLP回归,一个是Darknet53回归得到的。图的构建依旧是以检测框和目标作为节点,节点特征的更新则是:
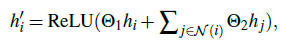
这里面要注意的是两个head,其中检测head的是根据各节点特征利用MLP降维得到用于分类和回归的特征。而数据关联head则是边权,它的确定是依据节点特征的差异,通过三层全连接得到的:
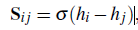
最终效果如下:

可以看到单纯用GNN做数据关联的提升并不大,当然,这里并没有做消融实验,也不能妄下评论。
参考文献
[1] Jiang X, Li P, Li Y, et al. Graph Neural Based End-to-end Data Association Framework for Online Multiple-Object Tracking[J]. arXiv preprint arXiv:1907.05315, 2019.
[2] Ma C, Li Y, Yang F, et al. Deep association: End-to-end graph-based learning for multiple object tracking with conv-graph neural network[C]//Proceedings of the 2019 on International Conference on Multimedia Retrieval. 2019: 253-261.
[3] Jiahe L, Xu G, Tingting J.Graph Networks for Multiple Object Trackin[C]//The IEEE Winter Conference on Applications of Computer Vision (WACV).2020.
[4] Brasó G, Leal-Taixé L. Learning a neural solver for multiple object tracking[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020: 6247-6257.
[5] Weng X, Wang Y, Man Y, et al. GNN3DMOT: Graph Neural Network for 3D Multi-Object Tracking with Multi-Feature Learning[J]. arXiv preprint arXiv:2006.07327, 2020.
[6] Weng X, Yuan Y, Kitani K. Joint 3d tracking and forecasting with graph neural network and diversity sampling[J]. arXiv preprint arXiv:2003.07847, 2020.
[7] Wang Y, Weng X, Kitani K. Joint Detection and Multi-Object Tracking with Graph Neural Networks[J]. arXiv preprint arXiv:2006.13164, 2020.

