前言
最近基于深度学习的多目标跟踪算法越来越多,有用于特征提取的,有改进单目标跟踪器的,也有提升数据关联的。如果真的要总结的话那就太多了,所以我准备分类别进行介绍,这次我主要介绍端到端的数据关联方法。其中ICCV2019Tracktor++的作者团队在CVPR2020上被录用的DeepMOT和MPN Tracker两篇就是专门研究端到端数据关联算法的,这次我们结合近两年的顶会文章进行讲解。后续的部分也会继续在我的专栏更新~
1.Deep affinity network for multiple object tracking(DAN)
作者:ShiJie Sun, Naveed Akhtar, HuanSheng Song, Ajmal Mian, Mubarak Shah
备注信息:PAMI2019
这是一篇创作于2017.9,并刊登于PAMI2019的端到端多目标跟踪框架,对于后续几篇文章都有着启示作用。DAN框架[1]很简洁新颖:
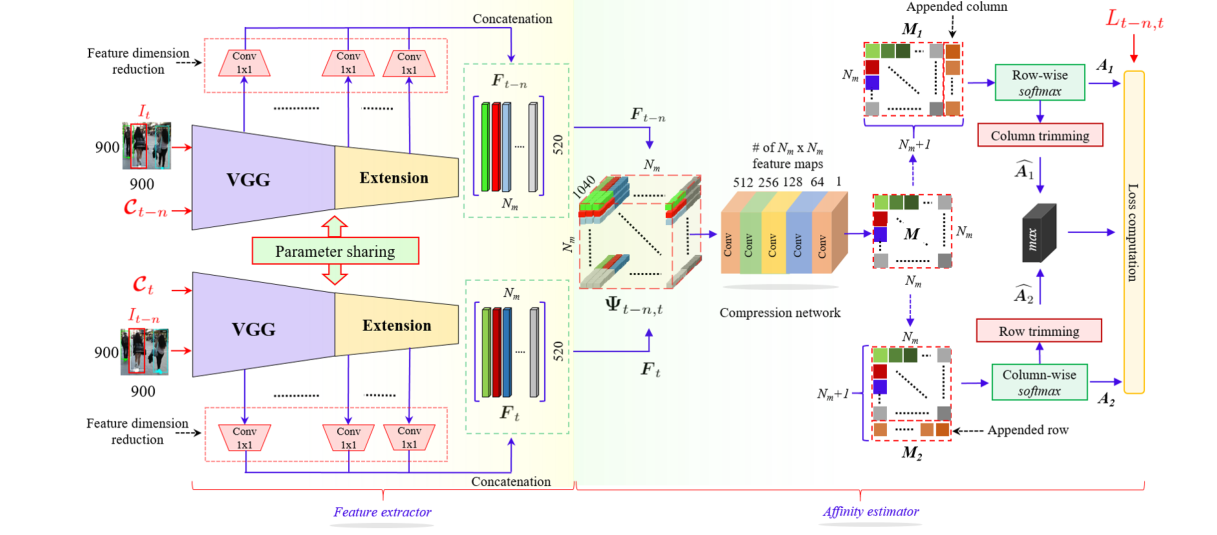
作者提出这个框架的目的是将表观特征和数据关联算法结合形状端到端的联合框架,在 NVIDIA GeForce GTX Titan上的效率为6.7FPS,下面我结合文章内容具体地解析算法。
1.1 数据准备与增强
要实现端到端的训练,如何将多目标跟踪数据集整理出来是第一大难关。这里作者采用了单目标跟踪算法中常用的跨帧匹配方式,允许相隔1~30帧的的视频帧进行跨帧数据关联,这样就可以解决MOT样本数量不足的问题。然而,视频类数据集还存在一个问题,即相邻帧的信息几乎一样,使得样本缺乏多样性。因此作者采用了几类数据增强方法:

作者在文中提到了三种数据增强方法:
- 光学扰动。即先将RGB图像转换到HSV格式,然后将S通道的每个值随机放缩[0.7,1.5],最后转换到RGB格式,并将值域约束到0~255或者0~1;
- 图像扩展放缩。本质上就是图像随机放缩,但是为了保证输入尺寸大小一致,作者在图像四周增加[1,1.2]倍的padding,padding像素值为图像均值;
- 随机裁剪。基于裁剪比例[0.8,1]在原图上裁剪,不过要求无论怎么裁剪,图像上所有目标框的中心点一定不能丢失,最后再放缩至指定尺寸。
而作者在代码中实际上使用了更复杂的数据增强方法:
1 | self.augment = Compose([ |
除去一些常规的数据类型转换和归一化操作,我们可以看到还多了一个随机水平镜像的操作RandomMirror,并且以上操作的概率为0.3。除此之外,熟悉MOT Challenge数据集的人应该知道,在该数据集中,无论目标是否可见都会标注,因此作者将可视度低于0.3的目标视为不可见,即认为不存在。另外,端到端的框架要保证输入输出的尺寸不变,因此作者设定了每一帧中出现的目标数量上限Nm,如80。
1.2特征提取器
特征提取器作为网络的第一个阶段,由上面的图示可以知道,作者利用孪生网络结构,通过特征提取器处理指定两帧中出现的所有目标框。特征提取器的结构为VGG网络+自定义扩展的结构组成:

为了利用多尺度多感受野信息,作者取了以上9层的特征图信息,得到了长度为520的特征向量,即60+80+100+80+60+50+40+30+20,可以看到520这个数据就是9层特征通道之和。不过文中作者并没有介绍是如何处理这些特征的,我们通过代码来观察:
1 | def forward_feature_extracter(self, x, l): |
从代码可以看到,9层不同分辨率的特征图都通过采样操作降维了,其中`source表示的是特征图BxCxHxW,labels表示的是一个框中心坐标BxNx1x1x2,也就是说每个特征图都会采样每个框的映射位置。因此最后通过得到就是Bx(CxN)的输出,也就是图中的Nmx520,这个过程的确挺出乎我意料的。
1.3亲和度估计
亲和度估计实际上就是特征相似度计算和数据关联过程的集成,第一步我们可以看到作者将两个520xNm大小的特征图变成了一个1040xNmxNm大小的亲和度矩阵,比较难理解:
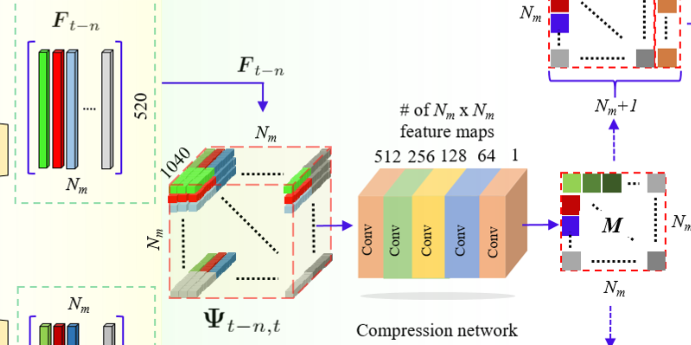
这里我们观察一下作者的代码:
1 | def forward_stacker2(self, stacker1_pre_output, stacker1_next_output): |
可以看到,作者的处理方式也比较特征先分别将两个520xNm大小的特征图分别扩展维度变成了520x1xNm和520xNmx1的矩阵,然后分别复制Nm次,得到两个520xNmxNm矩阵,最后将通道合并得到1040xNmxNm大小的特征矩阵。随后利用一系列1x1卷积降维至NmxNm大小。
作者在这里考虑了实际过程中出现的FP和FN情况,即目标轨迹无对应观测和观测无对应目标轨迹的场景,分别为关联矩阵的行列增加了一个x单元,用于存储这些情况,即L:(Nm+1)x(Nm+1)。
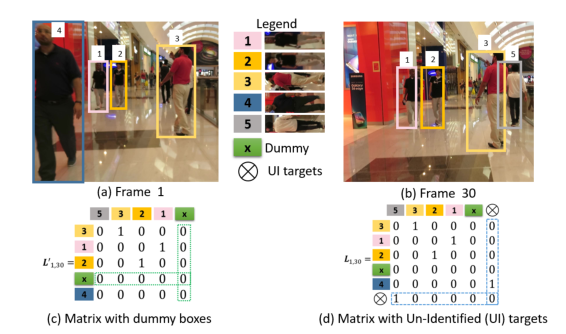
其中最后一行和最后一列都填充为固定值,文中作者设定的是10.
1.4训练
为了方便损失函数的设计,作者将L拆解为row-wise何column-wise两种形式:M1:Nmx(Nm+1)和M2:(Nm+1)xNm。并分别采用行softmax和列softmax求得各自的联合概率分布A1和A2两种分配矩阵。这里做一个解释,对于增加了一列的M1矩阵,其针对的是第t-n帧的目标轨迹和第t帧观测的匹配,通过行softmax可以得到每个目标属于每个观测的概率,这是一个前向的匹配过程。反之M2就是一个反向的匹配过程。
基于这种假设,作者设计了四种损失函数,分别是前向/反向损失、前向反向一致性损失和联合损失:
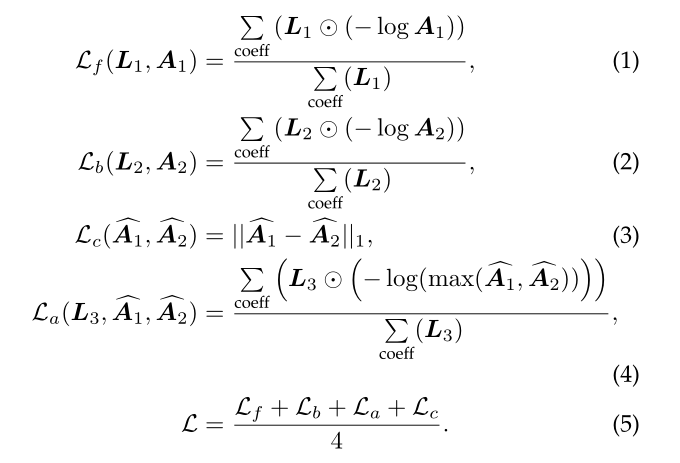
其中L1和L2是为了保证L和A1/A2矩阵尺寸一致所裁剪行列得到的矩阵。训练算法方面,作者采用的是multi-step的学习率下降策略,batchsize=8,epochs=120.
1.5推理
通过以上分析我们可以知道的是,该网络通过输入两帧的目标信息可以得到亲和度矩阵A=max(A1, A2),然而这个矩阵并不是关联矩阵,更像是相似度矩阵,并不能直接得到跟踪结果。然而作者并没有将相似度矩阵转换为代价矩阵输入匈牙利算法:

从文章可以看到,作者将目标轨迹i的历史帧信息与当前帧第j个目标的亲和度求和了,但是如何使用的还是没说清,这一点我们在代码里面找到了:
1 | def get_similarity_uv(self, t, frame_index): |
可以看到的是,除了亲和度矩阵,作者还加入了iou信息作为mask,然后利用iou_tracker的方式,采用贪婪算法,逐行取最大相似度的匹配,这种方式以及其变种我在之前的博客详细介绍过。没有引入其他的模块,如运动信息等,效果也不错:
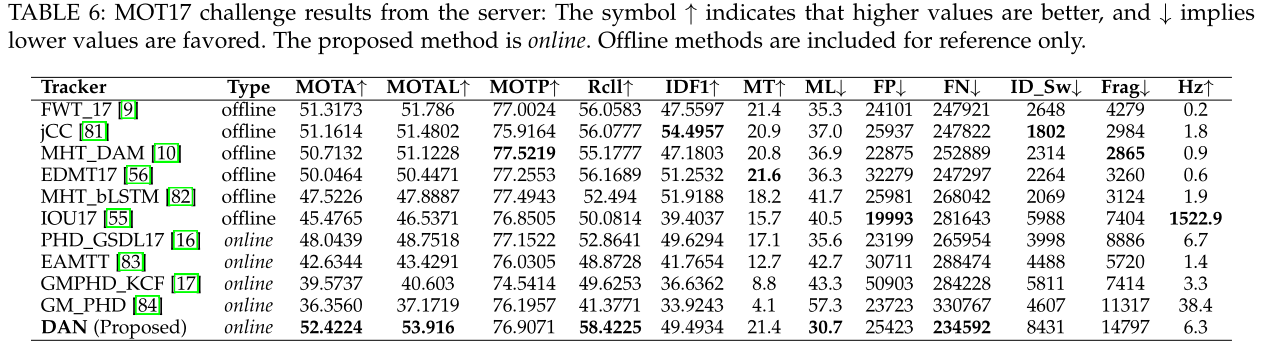
2.A Differentiable Framework for Training Multiple Object Trackers(DeepMOT)
作者:Yihong Xu, Aljosa Osep, Yutong Ban, Radu Horaud, Laura Leal-Taixé, Xavier Alameda-Pineda
备注信息:ICCV2019Tracktor++的作者团队,CVPR2020
这篇DeepMOT[2]文章作者团队与ICCV2019的Tracktor++[3]团队一致,不过这篇文章的创新性很高,内容也很精彩,所以我这里也详细介绍一下。
2.1匈牙利算法形式演化
作者一开始就交代了原始匈牙利算法的算法形式:
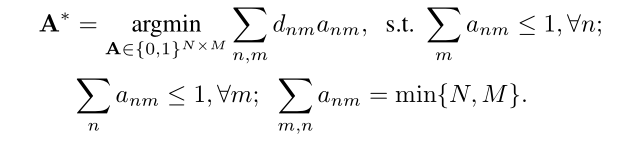
其中D表示代价矩阵,这里叫距离矩阵,A表示0-1分配矩阵,匈牙利算法的核心就是在保证每个轨迹最多只有一个观测,每个观测最多只有一个目标轨迹对应的前提下,是的代价最小。
紧接着,作者以MOT中常用的两个指标MOTA和MOTP为例进行微分化:
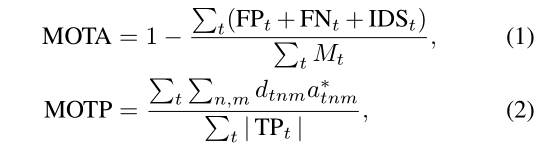
对于MOTP,作者这里没有给出原始的形式,不过我们将距离矩阵看做iou信息就可以啦,即MOTP统计的是所有跟踪正确的轨迹的IOU平均值。这里我们不妨直接介绍DeepMOT的损失函数:

可以看到,作者直接借助MOTA和MOTP指标,通过将其微分化得到了损失函数。其中要微分化就要将FP、FN、TP和ID Sw.等四个指标先微分化:
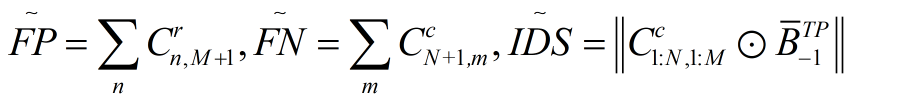
这里做一个解释,作者在设计关联矩阵的时候跟DAN一样,增加了一行一列,所以FP就是新增的目标观测信息被误匹配到了已存在的目标轨迹上,即最后一列的数值之和,同理可得FN。对于IDS,其意义在于目标轨迹中的身份切换次数,因此作者通过上一帧的关联0-1矩阵和当前帧估计的匹配矩阵C进行相乘。示例如下:
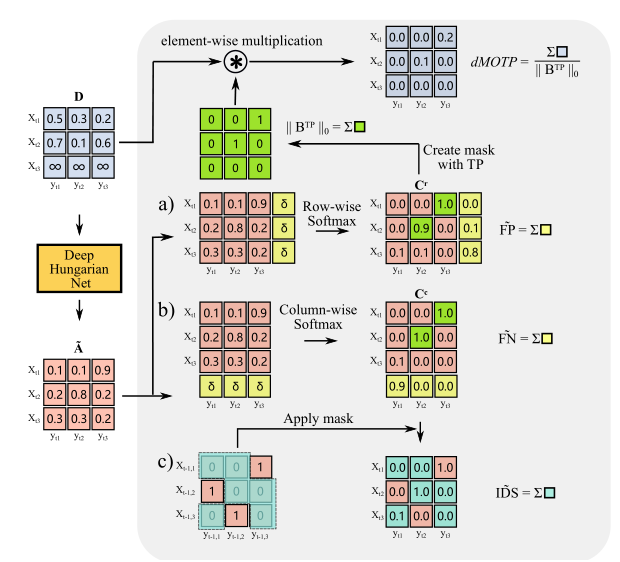
其中距离矩阵D的计算是根据关联结果,利用iou和欧氏距离计算而来:
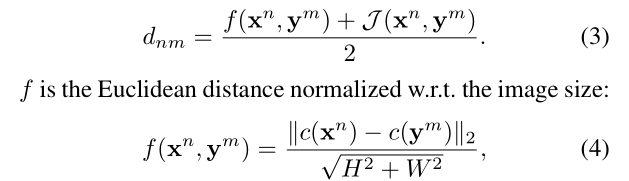
从上图可以得到一个有意思的信息,即关联矩阵大小可以不固定,不用预设目标数量。
2.2DHN网络设计
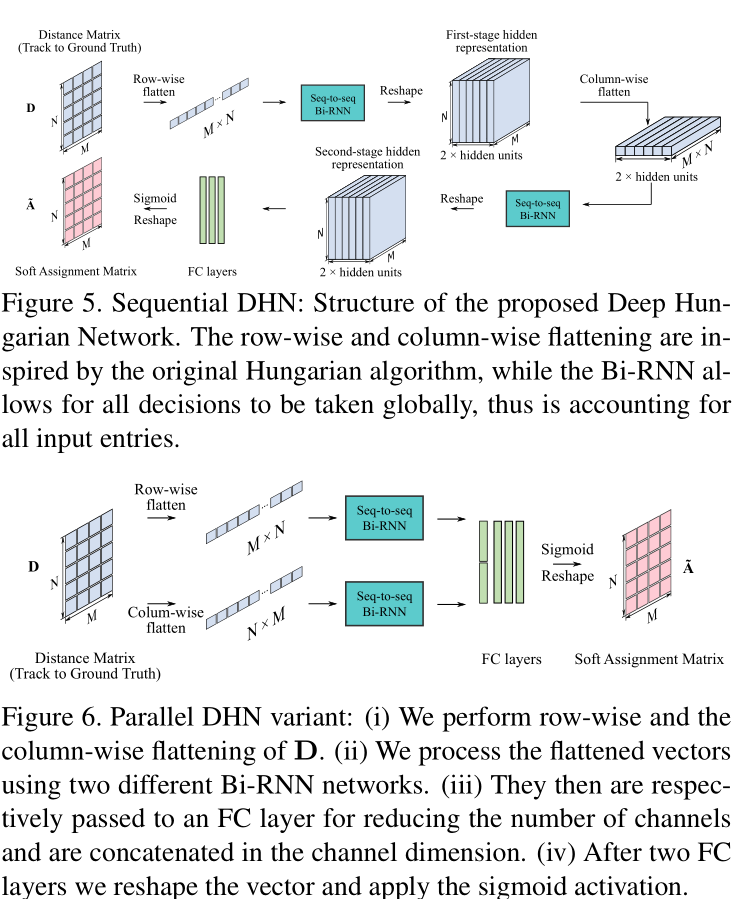
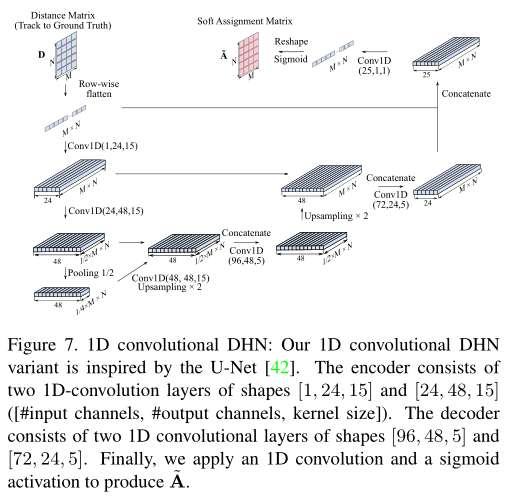
DHN网络是一个单独设计的网络框架,其输入是目标轨迹和观测量的距离矩阵,在训练的时候作者直接采用了public detections作为目标轨迹,gt作为观测。可以看到的是,作者通过两个阶段的特征变换,使得两两之间的相似度信息得到了充分交互。这里作者设计了三种流程,一种是串行的Sequential模式,一种是并行的Parallel模式,最后一种是基于U-Net的形式,利用卷积网络进行交互。其中row-wise的意思是一行行的从NxM的距离矩阵中取向量,得到1x(MN)的向量。
而对于向量中各单元的交互,作者采用了Seq2Seq的BiRNN结构:

但是我从文中不明白的是,作者如何将一个1x(MN)的向量,通过Seq2Seq转换为2HxNxM的矩阵的。这里我去看了一下代码:
1 | self.lstm_row = nn.GRU(element_dim, hidden_dim, bidirectional=biDirenction, num_layers=2) |
备注:element_dim为1,hidden_dim为256。也就是说输入一个长为NM的序列,得到NMx512的输出。
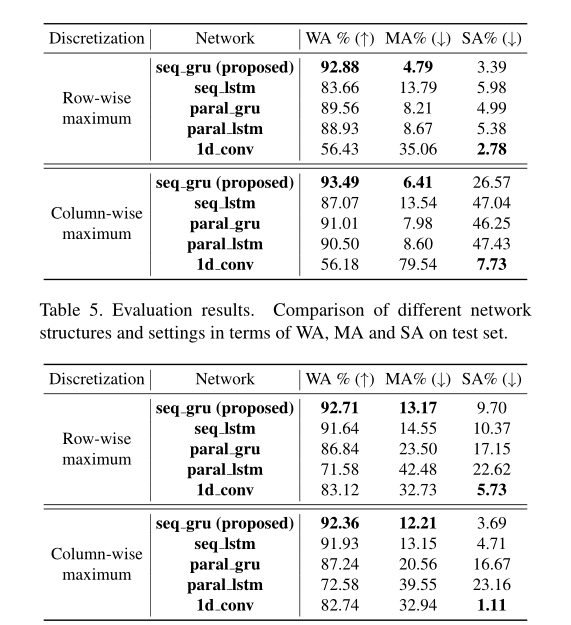
可以看到基于Sequential流程和GRU结构的框架效果最好,其中WA指的是准确率,MA指的是未被分配到观测信息的比例,SA指的是分配超过一个观测信息的比例。
2.3实现细节
对于填充行列的固定值,作者采用的是0.5,另外,由于关联矩阵是离散且稀疏的,所以作者首先通过sigmoid离散化0-1矩阵,然后基于关联矩阵中的0-1数量比例进行自适应的损失加权。采用RMSprop优化器,初始学习率为3e-4,每2w iter降低5%学习率,训练20epochs,只用6小时。gt是通过匈牙利算法生成的。
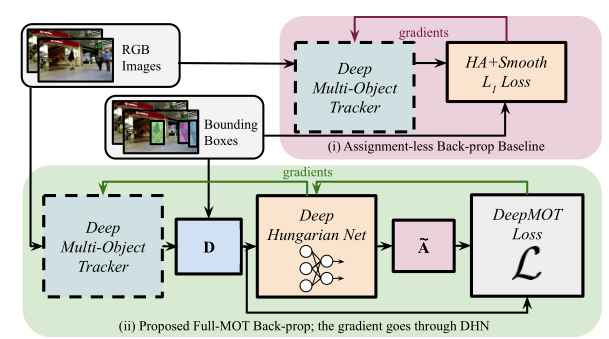
作者的底层多目标跟踪框架是Tracktor++构建的,在此基础上加入了ReID head,从而实现多任务的训练模式。其中Re-ID分支采用ResNet50网络结构,通过triplet loss训练。除此之外,作者还尝试利用单目标跟踪算法SiamRPN和GOUTRN作为底层跟踪器进行实现,可以发现,DeepMOT均有所帮助。

为了降低过拟合风险,作者还将标注的目标框信息进行一定尺度的放缩和平移,增大误差,模拟实际观测误差。
3.Online multi-object tracking with dual matching attention networks(DMAN)
作者:Ji Zhu,Hua Yang,Nian Liu,Minyoung Kim,Wenjun Zhang ,and Ming-Hsuan Yang
备注信息:ECCV2018
DMAN[4]和FAMNet[5]我本来准备放到下一讲SOT专题来讲的,但是考虑到篇幅平衡,并且这两个都可以扯到端到端的SOT+Data Association框架,就还是加进来了。
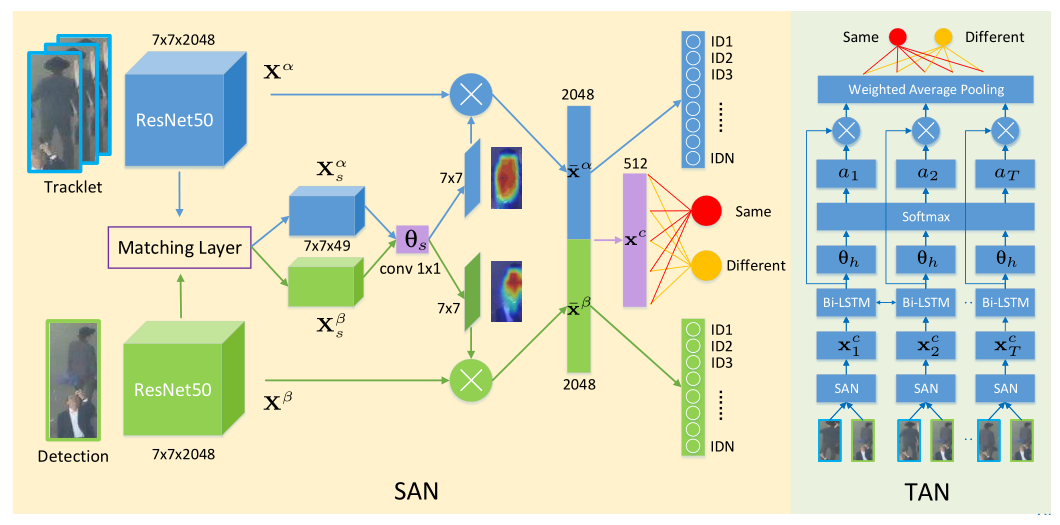
DMAN算法是基于以下四个方向展开的讨论:
通过空间注意力模块让网络更加注意前景目标:
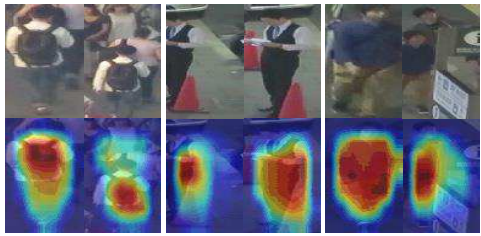
基于循环网络,利用时间注意力机制分析目标轨迹中各个历史信息的权重:

利用SOT跟踪器,缓解MOT中由于遮挡、观测信息质量不高导致的目标丢失等情况,增强鲁棒性。
其中空间注意力模块很简单,就是深度学习中常见的mask,利用mask与原特征图进行相乘。而时间注意力网络,则是将目标轨迹中的所有的历史信息与当前观测信息进行匹配,最后加权判断是否匹配成功。
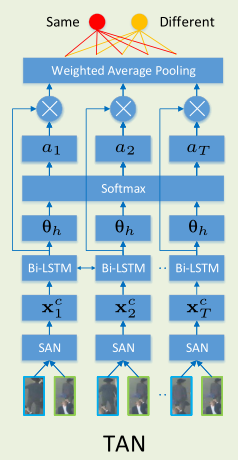
而SOT跟踪器的底层算法是单目标跟踪中知名的ECO算法,不过作者考虑到背景和前景的样本不平衡问题,引入代价敏感参数q(t)对其进行了进一步的改进:
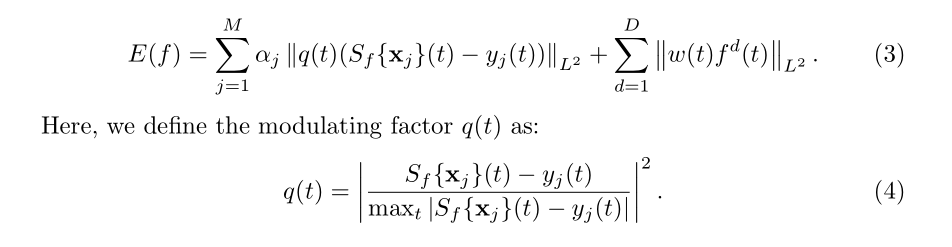
之所以我要将DMAN算做端到端的数据关联框架,是因为这个框架实现的是1:N的数据关联,这里有两层含义:
- 一个观测对应N个轨迹历史信息;
- 一个观测对应N条目标轨迹,这里是以batch的形式实现的,勉强沾边吧。
4.Joint learning of feature, affinity and multi-dimensional assignment for online multiple object tracking(FAMNet)
作者:Peng Chu, Haibin Ling
备注信息:ICCV2019
相比于DMAN,FAMNet[4]对于端到端数据关联算法的集成更加紧密:
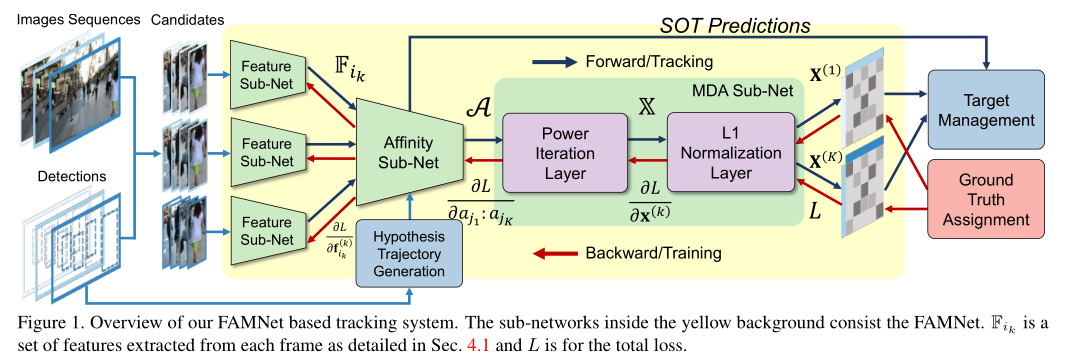
通过观察网络可以看到,FAMNet的流程是SOT->Affinity->Data Association->post process,其中它的核心在于通过局部的关联形式完成了K帧的联合数据关联训练。
4.1Affinity Subnet
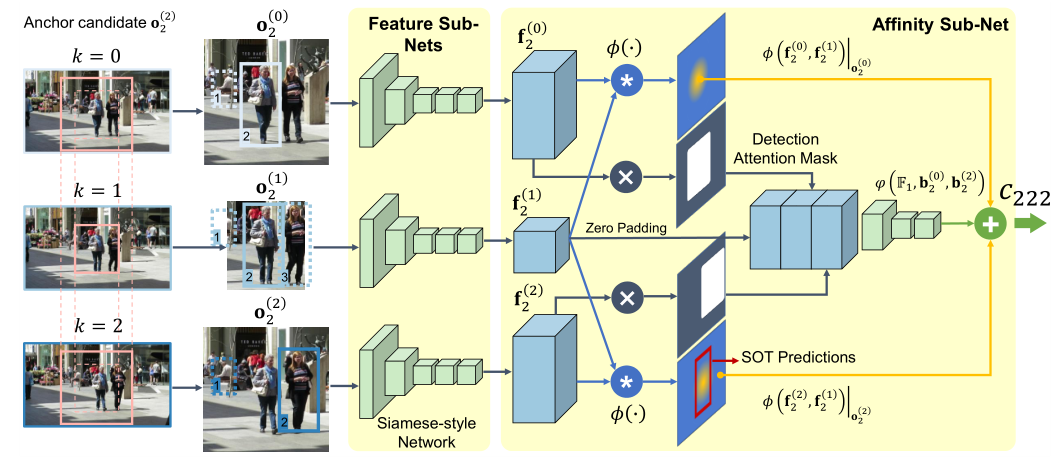
作者将SOT孪生网络和亲和度网络合并,SOT backbone作为特征提取器,SOT输出的置信图作为亲和度依据。下面我们详细分析一下这个网络结构。
作者这里提出了一个新概念anchor candidate,这里指的是当前帧的目标,对应上图中中间部分k=1的分支,至于途中所提到的数字2,这里指的是当前帧中的第二个目标。对于指定目标,通过对当前帧和前后帧扩展区域的裁剪,基于两个孪生网络进行两次SOT跟踪流程,从而得到上下两个置信图输出。
这其中还有三个Detection Attention Mask,初步理解就是将观测信息变成mask,而观测信息的确定是通过目标序号来确定的,所以可以看到观测信息并非与当前目标对应。最终得到的亲和度就是两个SOT置信图得到的信息和detection mask得到的亲和度之和,在上面的例子里面存在3x3x3对亲和度,但是由于两个非`anchor frame并没有直接参与匹配,所以图中显示的是C222。这里作者借鉴的是IJCAI2019的一篇论文的策略[6]:
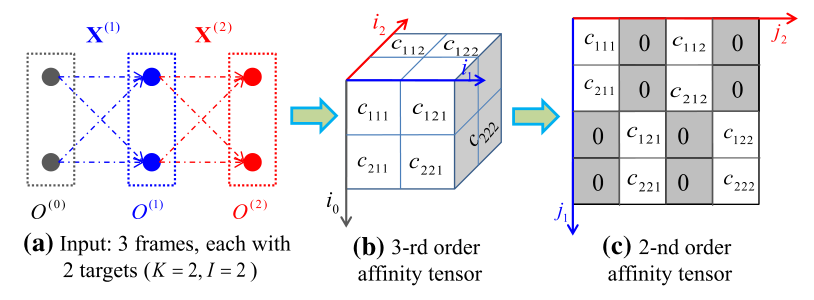
4.2 R1TA Power Iteration Layer
对于关联假设的生成,FAMNet采用了与前文一致的策略:
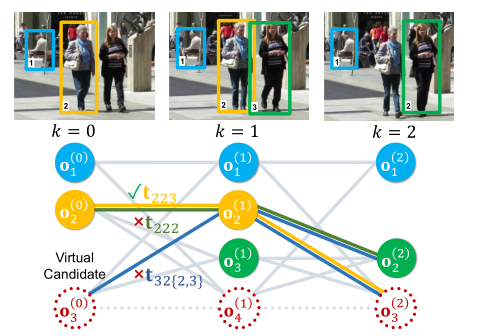
那么从亲和度矩阵到数据关联的集成,作者同样借鉴了IJCAI2019的那篇论文的策略[6],首先将匈牙利算法进行了重构:

即将整体的数据关联n:m,变成了n份小型的数据关联的联合作用,对于这个关系的转换,可以参照论文[6]:
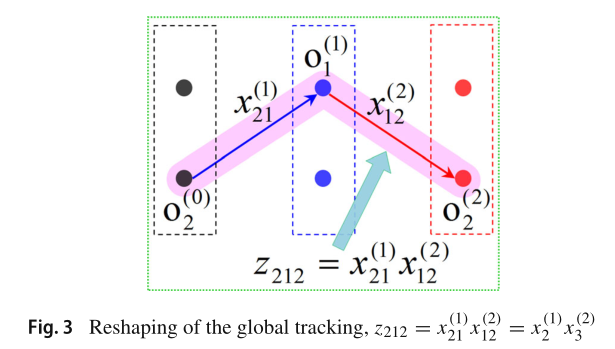
其中z_212指的是第一帧中的第二个目标、第二帧中的第一个目标和第三帧中的第二个目标的整体关联结果是否为真,其中任意一对不成立都会变成0。然后基于R1TA Power Iteration过程,将这种多次SOT过程组成一个完整的数据关联过程:
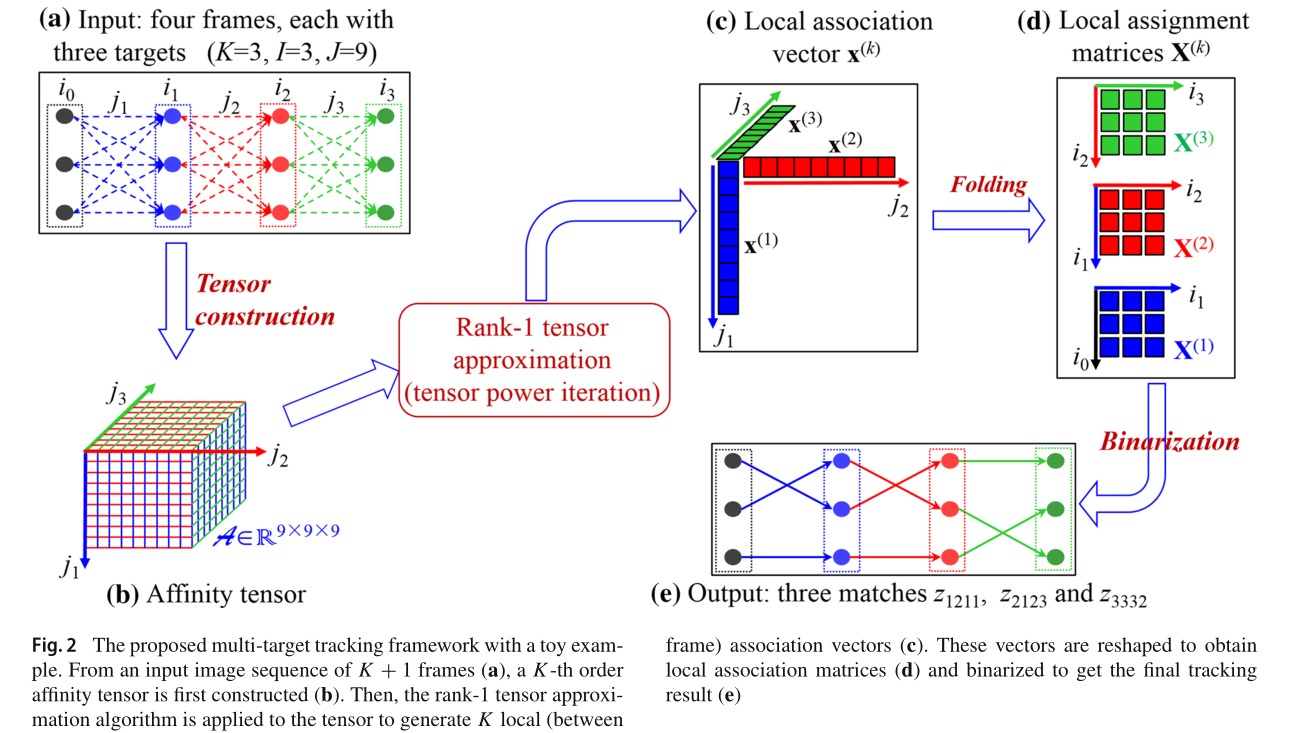
经过我们上面的讨论,这幅图里面的大多数的示意应该能懂,但是对于Rank-1 tensor approximation可能还有疑惑,文中也给出了解释,我感觉这两篇几乎就是理论和实践分开投了两个顶会…

可以看到,作者通过一个连续的外积公式来近似k阶关联矩阵,从而转换了匈牙利算法问题形式。作者也给出了迭代算法的前向反向公式:

可以注意到的是,这里面有一个除法因子,用作L1 norm,作者也给出了它的求导转换,这里我就不再放了。
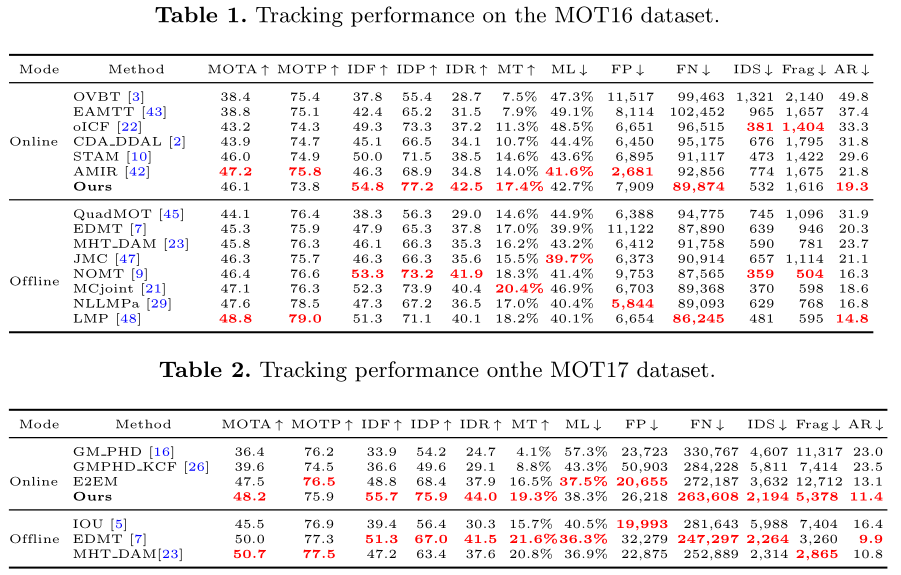
结果如下:
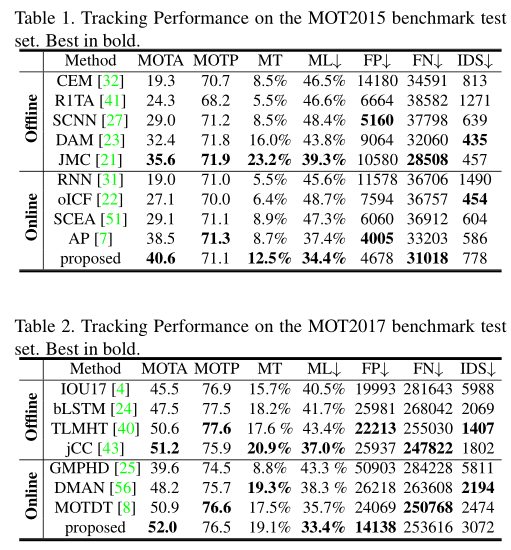
5.Learning a Neural Solver for Multiple Object Tracking(MPNTracker)
作者:Brasó G, Leal-Taixé L
备注信息:MOT Challenge上前列,CVPR2020
论文链接:https://arxiv.xilesou.top/pdf/1912.07515
代码链接:https://github.com/selflein/GraphNN-Multi-Object-Tracking
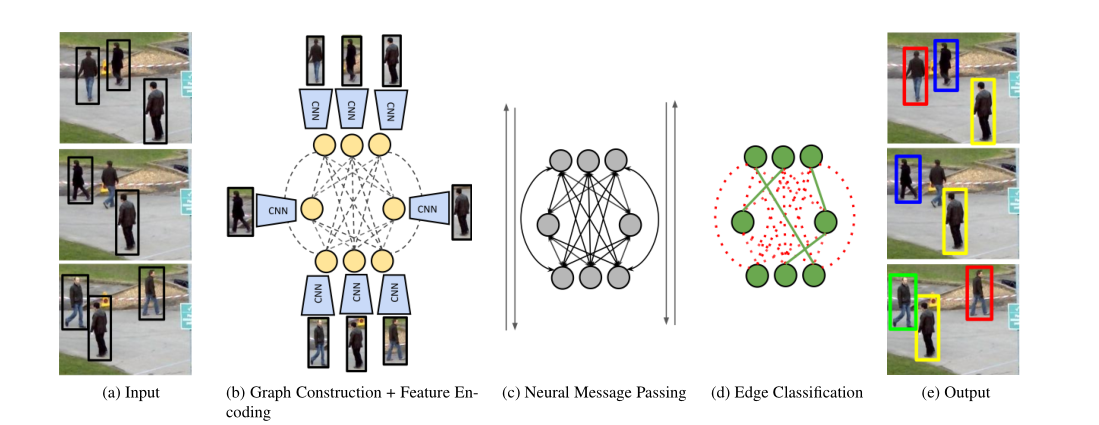
MPNTracker在MOT Challenge各个榜单上都位于前列,不过近期有个别算法超过去了,但是它的各项指标性能依旧很高。这个算法框架很简洁,直接借助了图卷积网络中的消息传递机制,基于Re-ID和位置形状信息进行特征建模,不过我暂时对于图卷积不是很了解,所以就不做详细的介绍:
对于当前帧的每个目标,其消息传递方式的节点更新部分考虑了时间信息,即针对前面的帧和后面的帧,分开计算边的累加影响,利用链接的方式结合,而非累加的方式。
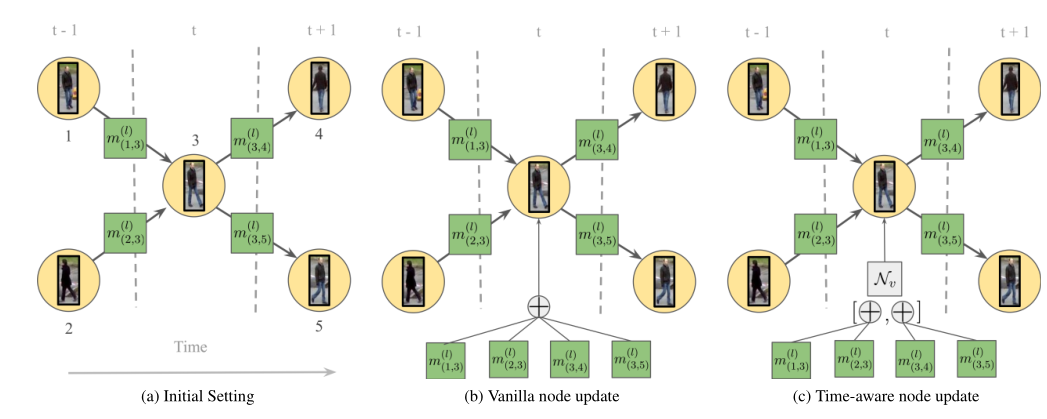
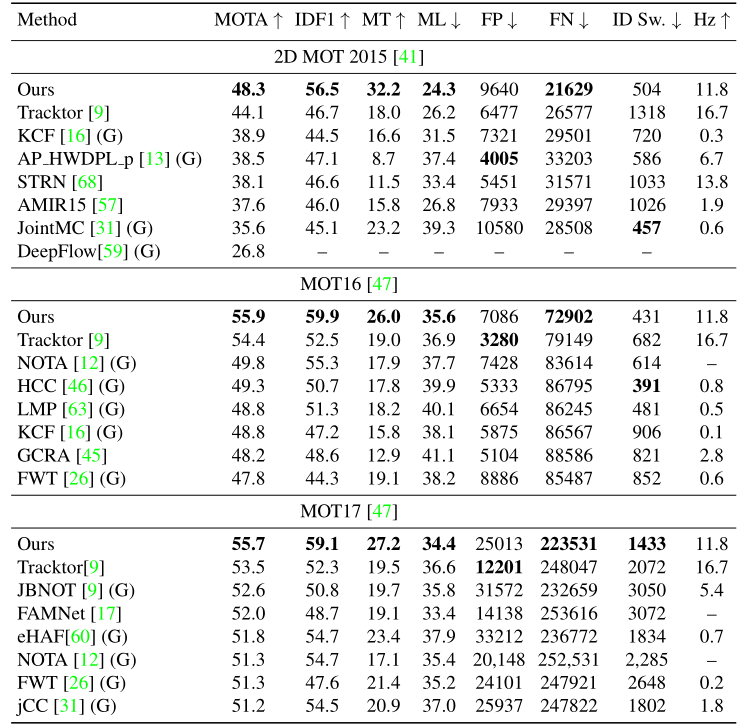
可以看到,整体结构很简单,就是网络的构建和特征的建模,其中网络构建部分我在之前的博客中进行了详细的介绍。其效果也很不错:
参考文献
[1] Sun S, Akhtar N, Song H, et al. Deep affinity network for multiple object tracking[J]. IEEE transactions on pattern analysis and machine intelligence, 2019.
[2] Xu Y, Ban Y, Alameda-Pineda X, et al. DeepMOT: A Differentiable Framework for Training Multiple Object Trackers[J]. arXiv preprint arXiv:1906.06618, 2019.
[3] Bergmann P, Meinhardt T, Leal-Taixe L. Tracking without bells and whistles[C]. in: Proceedings of the IEEE International Conference on Computer Vision. 2019. 941-951.
[4] Zhu J, Yang H, Liu N, et al. Online multi-object tracking with dual matching attention networks[C]. in: Proceedings of the European Conference on Computer Vision (ECCV). 2018. 366-382.
[5] Chu P, Ling H. Famnet: Joint learning of feature, affinity and multi-dimensional assignment for online multiple object tracking[C]. in: Proceedings of the IEEE International Conference on Computer Vision. 2019. 6172-6181.
[6]X. Shi, H. Ling, Y. Pang, W. Hu, P. Chu, and J. Xing. Rank-1 tensor approximation for high-order association in multi-target tracking. IJCV, 2019.
[7] Brasó G, Leal-Taixé L. Learning a Neural Solver for Multiple Object Tracking[J]. arXiv preprint arXiv:1912.07515, 2019.

